题目内容
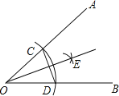
【题目】如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D,再分别以点C、D为圆心,大于![]() CD的长为半径画弧,两弧在∠AOB内部交于点E,作射线OE,连接CD,以下说法错误的是( )
CD的长为半径画弧,两弧在∠AOB内部交于点E,作射线OE,连接CD,以下说法错误的是( )
A.△OCD是等腰三角形B.CD垂直平分OE
C.点E到OA、OB的距离相等D.证明射线OE是角平分线的依据是SSS
【答案】B
【解析】
由题干的整体描述可知是角平分线的做法,由“以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D”可知OC=OD,由“分别以点C、D为圆心,大于![]() CD的长为半径画弧,两弧在∠AOB内部交于点E”可知CE=CD,由图可知OE为公共边,所以△OCE≌△ODE,四个选项可以依次验证排除选出答案
CD的长为半径画弧,两弧在∠AOB内部交于点E”可知CE=CD,由图可知OE为公共边,所以△OCE≌△ODE,四个选项可以依次验证排除选出答案
由“以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D”可知OC=OD,所以选项A正确,由“分别以点C、D为圆心,大于![]() CD的长为半径画弧,两弧在∠AOB内部交于点E”可知CE=CD,由图可知OE为公共边,所以△OCE≌△ODE(SSS)所以选项D正确,因为△OCE≌△ODE,所以∠COE=∠DOE,所以OE是∠AOB的角平分线,所以C选项正确,所以最后本题选B
CD的长为半径画弧,两弧在∠AOB内部交于点E”可知CE=CD,由图可知OE为公共边,所以△OCE≌△ODE(SSS)所以选项D正确,因为△OCE≌△ODE,所以∠COE=∠DOE,所以OE是∠AOB的角平分线,所以C选项正确,所以最后本题选B

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目