题目内容
【题目】如图,在直角坐标系中, B(0,8),D(10,0),一次函数y=![]() x+
x+![]() 的图象过C(16,n),与x轴交于A点。
的图象过C(16,n),与x轴交于A点。
(1)求证:四边形ABCD为平行四边形;
(2)将△AOB绕点O顺时针旋转,旋转得△A1OB1,问:能否使以点O、A1、D、B1为顶点的四边形是平行四边形?若能,求点A1的坐标;若不能,请说明理由;

【答案】(1)见解析;(2)能,所求满足条件的A1为:(―![]() ,
, ![]() )、(
)、(![]() ,
, ![]() )、(
)、(![]() ,―
,―![]() )
)
【解析】整体分析:
(1)把点过C(16,n)代入到y=![]() x+
x+![]() ,求出n,得到点C的坐标,求出点A的坐标,由AD与BC平行且相等证明;(2)分三种情况讨论,有两种是A1B1与OD平行,一种是A1B1与OD相交,结合平行四边形的性质和勾股定理求解.
,求出n,得到点C的坐标,求出点A的坐标,由AD与BC平行且相等证明;(2)分三种情况讨论,有两种是A1B1与OD平行,一种是A1B1与OD相交,结合平行四边形的性质和勾股定理求解.
解:(1)∵y=![]() x+
x+![]() 的图象过C(16,n),A两点,∴n=
的图象过C(16,n),A两点,∴n=![]() ×16+
×16+![]() =8,
=8,
∴C(16,8),A(-6,0).
∵B(0,8),∴BD∥x轴,
又∵AD=10―(―6)=16=BC,
∴四边形ABCD为平行四边形
(2)由题意可知;AB=A1B1=10,∠AOB=∠A1OB1=90°
①△AOB旋转后,若A1B1∥x轴,构成四边形OA1B1D如图①,
又∵A1B1=OD=10,∴四边形OA1B1D构成平行四边形,
此时,设A1B1与y轴交于H,
则OH=![]() =
=![]() ,A1H=
,A1H=![]() =
=![]() ,
,
∴A1(―![]() ,
, ![]() ).
).

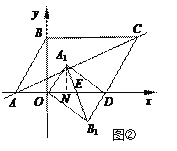
②△AOB旋转后,若A1B1的中点E在x轴上,构成四边形OA1DB1如图②.
∵∠A1OB1=90°,∴OE=![]() A1B1=5,∴OE=ED=5,
A1B1=5,∴OE=ED=5,
∴四边形OA1DB1构成平行四边形,
设作A1N⊥x轴交于N,∠A1OB1=∠OA1D=90°.
则AN=![]() =
=![]() ,ON=
,ON=![]() =
=![]() ,
,
∴A1(![]() ,
, ![]() ).
).
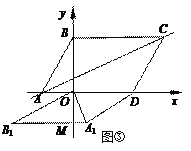
③△AOB旋转后,若A1B1∥x轴,构成四边形ODA1B1如图③,
又∵A1B1=OD=10,∴四边形ODA1B1构成平行四边形,
此时,设A1B1与y轴交于M,
则OM=![]() =
=![]() ,A1M=
,A1M=![]() =
=![]() ,
,
∴A1(![]() ,―
,―![]() ).
).
综上所述,所求满足条件的A1为(―![]() ,
, ![]() )、(
)、(![]() ,
, ![]() )、(
)、(![]() ,―
,―![]() )
)

 阅读快车系列答案
阅读快车系列答案





