题目内容
已知等腰三角形的内角是40°,则另外两个内角的度数分别是( )
| A.70°,70° | B. 70°,70°或40°,100° |
| C.40°,40° | D. 40°,70° |
B
已知给出了一个内角是40°,没有明确是顶角还是底角,所以要进行分类讨论,分类后还需用三角形内角和定理去验证每种情况是不是都成立.
解:分情况讨论:
(1)若等腰三角形的顶角为40°时,另外两个内角=(180°-40°)÷2=70°;
(2)若等腰三角形的底角为40°时,它的另外一个底角为40°,顶角为180°-40°-40°=100°.
故另外两个内角的度数分别为:40°、100°或70°、70°.
故选B.
本题考查了等腰三角形的性质及三角形的内角和定理;若题目中没有明确顶角或底角的度数,做题时要注意分情况进行讨论,这是十分重要的,也是解答问题的关键.
解:分情况讨论:
(1)若等腰三角形的顶角为40°时,另外两个内角=(180°-40°)÷2=70°;
(2)若等腰三角形的底角为40°时,它的另外一个底角为40°,顶角为180°-40°-40°=100°.
故另外两个内角的度数分别为:40°、100°或70°、70°.
故选B.
本题考查了等腰三角形的性质及三角形的内角和定理;若题目中没有明确顶角或底角的度数,做题时要注意分情况进行讨论,这是十分重要的,也是解答问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
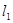 为
为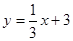 与直线
与直线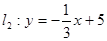 相交于A点,直线
相交于A点,直线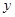 轴于B点,直线
轴于B点,直线 交
交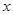 轴于C点,求 ① A点的坐标; ② △ABC的面积。
轴于C点,求 ① A点的坐标; ② △ABC的面积。

 的绳子围成一个长方形,且长方形的长比宽长10
的绳子围成一个长方形,且长方形的长比宽长10
 与
与 互余,且
互余,且 ,则
,则