题目内容
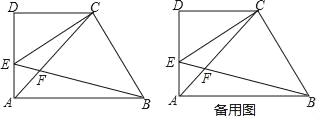
【题目】如图所示,已知AC∥BD,EA,EB分别平分∠CAB和∠DBA,CD过E点.求证:AB=AC+BD.

【答案】证明见试题解析.
【解析】
试题分析:在AB上取一点F,使AF=AC,连结EF,就可以得出△ACE≌△AFE,就有∠C=∠AFE.由平行线的性质就有∠C+∠D=180°,由∠AFE+∠EFB=180°得出∠EFB=∠D,在证明△BEF≌△BED就可以得出BF=BD,进而就可以得出结论.
试题解析:证明:在AB上取一点F,使AF=AC,连结EF.
∵EA、EB分别平分∠CAB和∠DBA,∴∠CAE=∠FAE,∠EBF=∠EBD.∵AC∥BD,∴∠C+∠D=180°.在△ACE和△AFE中,∵AC=AF,∠CAE=∠FAE,AE=AE,∴△ACE≌△AFE(SAS),∴∠C=∠AFE.∵∠AFE+∠EFB=180°,∴∠EFB=∠D.在△BEF和△BED中,∵∠EFB=∠D,∠EBF=∠EBD,BE=BE,∴△BEF≌△BED(AAS),∴BF=BD.∵AB=AF+BF,∴AB=AC+BD.

练习册系列答案
相关题目