题目内容
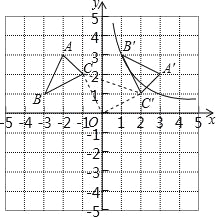
【题目】已知A(2,0),B(2,4),定义:若平面内点P关于直线AB的对称点Q在图形M内或图形的边界上,则称点P是图形M关于直线AB的“反称点”.
(1)已知C(5,0),D(5,3)
①点M1(0,3),M2(-0. 5,2),M3(-2,1),则是△ACD关于直线AB的“反称点”的是________:
②若直线y=2x+m上存在△ACD关于直线AB的“反称点”,求m的取值范围;
(2)已知点E(1,0),F(5,0), ![]() ,点P(x,y)在直线y=x+1上,且点P是△EFG的反称点,求点P横坐标的取值范围.
,点P(x,y)在直线y=x+1上,且点P是△EFG的反称点,求点P横坐标的取值范围.
【答案】(1)①M2;②-4≤m≤5(2)![]()
【解析】试题分析:根据“反称点”的定义解答即可.
试题解析:解:(1)①设直线AD的解析式为y=kx+b,则: ![]() ,解得:
,解得: ![]() ,∴直线AD为:y=x-2.点M1(0,3)关于直线AB的对称点为Q(4,3),当x=4时,y=x-2=2.∵2<3,∴Q在△ACD外,∴M1不是△ACD关于直线AB的“反称点”;
,∴直线AD为:y=x-2.点M1(0,3)关于直线AB的对称点为Q(4,3),当x=4时,y=x-2=2.∵2<3,∴Q在△ACD外,∴M1不是△ACD关于直线AB的“反称点”;
点M2(-0.5,2)关于直线AB的对称点为Q(4.5,2),当x=4.5时,y=x-2=2.5.∵2.5>2,∴Q在△ACD内,∴M2是△ACD关于直线AB的“反称点”;
点M3(-2,1)于直线AB的对称点为Q(6,1).∵6>5,∴Q在△ACD外,∴M3不是△ACD关于直线AB的“反称点”;
②设M(a,2a+m)在直线y=2x+m上,M关于直线AB的对称点为 Q(4-a,2a+m),则2≤4-a≤5,0≤2a+m≤2-a,解得:-1≤a≤2,-4≤m≤5;
(2)易求直线EF的解析式为![]() .点P(a,a+1)在直线y=x+1上,P关于直线AB的对称点为Q(4-a,a+1),则1≤4-a≤5,0≤a+1≤
.点P(a,a+1)在直线y=x+1上,P关于直线AB的对称点为Q(4-a,a+1),则1≤4-a≤5,0≤a+1≤![]() ,解得:-1≤a≤
,解得:-1≤a≤![]() .
.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案【题目】某班组织了一次读书活动,统计了16名同学在一周内的读书时间,他们一周内的读书时间累计如表,则这16名同学一周内累计读书时间的中位数是 .
一周内累计的读书时间(小时) | 5 | 8 | 10 | 14 |
人数(个) | 1 | 7 | 5 | 3 |