题目内容
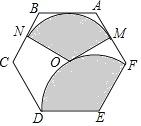
【题目】用一条直线截三角形的两边,若所截得的四边形对角互补,则称该直线为三角形第三条边上的逆平行线.如图![]() ,
,![]() 为
为![]() 的截线,截得四边形
的截线,截得四边形![]() ,若
,若![]() ,则称
,则称![]() 为
为![]() 边
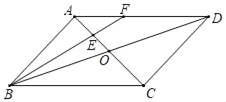
边![]() 的逆平行线;如图
的逆平行线;如图![]() ,已知
,已知![]() 中,
中,![]() ,过
,过![]() 边上的点
边上的点![]() 作
作![]() 交于点
交于点![]() ,过点
,过点![]() 作边
作边![]() 的逆平行线
的逆平行线![]() ,交
,交![]() 边于点
边于点![]() .
.
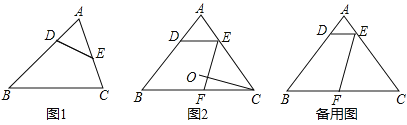
(1)求证:![]() 是边
是边![]() 的逆平行线.
的逆平行线.
(2)![]() 点是
点是![]() 的外心,连接
的外心,连接![]() ,求证:
,求证:![]() .
.
(3)已知![]() ,
,![]() ,过点
,过点![]() 作边
作边![]() 的逆平行线
的逆平行线![]() ,交边
,交边![]() 于点
于点![]() .
.
①试探索![]() 为何值时,四边形
为何值时,四边形![]() 的面积最大,并求出最大值;
的面积最大,并求出最大值;
②在①的条件下,比较![]()
![]() 大小关系.(“
大小关系.(“![]() 或
或![]() ”)
”)
【答案】(1)见解析;(2)见解析;(3)①![]() ,最大值
,最大值![]() ;②=
;②=
【解析】
(1)由条件可证得∠B=∠ACB,则∠BDE+∠B=180![]() .∠BDE+∠ACB=180
.∠BDE+∠ACB=180![]() ,结论得证;
,结论得证;
(2)连接AO,BO,证得∠FEC=∠B,由OA=OC可得∠OAC=∠OCA,∠BAO=∠OAC,证出![]() ,即CO⊥FE,
,即CO⊥FE,
(3)①设FC=x,则BF=6x,证△FEC∽△ABC,可得![]() ,同理可得
,同理可得![]() ,四边形AGFE的面积可表示为S△ABCS△EFCS△BFG,利用二次函数的性质可求出最大值,得到点F为BC的中点,连接DF,根据EF为AB边的逆平行线,可证得DF为AC边的逆平行线, 得到G点与D点重合,再根据相似三角形的判定与性质求出AD的长;
,四边形AGFE的面积可表示为S△ABCS△EFCS△BFG,利用二次函数的性质可求出最大值,得到点F为BC的中点,连接DF,根据EF为AB边的逆平行线,可证得DF为AC边的逆平行线, 得到G点与D点重合,再根据相似三角形的判定与性质求出AD的长;
②由①知G点与D点重合,故可得到AD+BG=AB.
(1)证明理由如下:
![]()
![]()
![]()
![]()
![]()
![]() 边
边![]() 是的逆平行线;
是的逆平行线;
(2)如图1,连接![]() ,BO
,BO
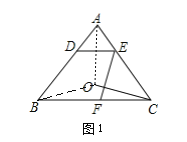
![]() 是边
是边![]() 的逆平行线
的逆平行线
![]()
![]()
![]()
![]() 点
点![]() 是
是![]() 的外心
的外心
![]() =BO,
=BO,
![]()
![]() ,AO=AO
,AO=AO
∴△ABO≌△ACO
![]() ,
,![]()
![]()
![]()
![]() ;
;
(3)如图2,作AQ⊥BC
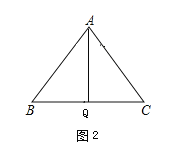
∵AB=AC,
∴AQ⊥BC,BQ=CQ=3
∴AQ=![]()
S△ABC=![]() =
=![]() =12,
=12,
①设![]() ,
,![]() ,
,![]()
∵∠FEC=∠B,∠FCE=∠ACB,
∴△FEC∽△ABC.
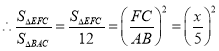
![]() ,
,
同理可得∠BGF=∠C,∠FBG=∠ABC
∴△FBG∽△ABC

∴![]()
![]() =
=![]() (x3)2+
(x3)2+![]() ,
,
当![]() 时,此时
时,此时![]() 有最大值,最大值为
有最大值,最大值为![]() ,
,
∴CF=BF=3,
如图3,连接DF,
∵BF=CF,∠B=∠C,BD=CE,
∴△BDF≌△CEF(SAS),
∴∠BDF=∠CEF,∠BFD=∠EFC,
∴∠BFE=∠DFC,∠AEF=∠ADF.
∵∠AEF+∠B=180![]() ,∠A+∠BFE=180
,∠A+∠BFE=180![]() ,
,
∴∠C+∠ADF=180![]() ,∠A+∠DFC=180
,∠A+∠DFC=180![]() .
.
∴FD为边AC的逆平行线,
由题意可知D与G点重合,
由![]() =
=![]()
过D点作DH⊥BC,
∴![]() BF×DH=
BF×DH=![]() ,故
,故![]() ×3×DH=
×3×DH=![]()
解得DH=![]()
∵AF∥DH
∴△BDH∽△BAF,设AD=a
∴BD=5-a
∴![]()
故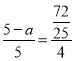
解得a=![]()
故![]() ,四边形
,四边形![]() 的面积最大值为
的面积最大值为![]() ;
;
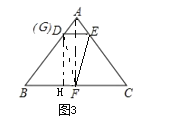
②由①可得D与G点重合,
∴AD+BG=AB,
故答案为:=.

 寒假学与练系列答案
寒假学与练系列答案【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:
成绩x 学校 |
|
|
|
|
|
甲 | 4 | 11 | 13 | 10 | 2 |
乙 | 6 | 3 | 15 | 14 | 2 |
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b.甲校成绩在![]() 这一组的是:
这一组的是:
70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校 | 平均分 | 中位数 | 众数 |
甲 | 74.2 | n | 5 |
乙 | 73.5 | 76 | 84 |
根据以上信息,回答下列问题:
(1)写出表中n的值;
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是_____________校的学生(填“甲”或“乙”),理由是__________;
(3)假设乙校800名学生都参加此次测试,估计成绩优秀的学生人数.
【题目】下表显示的是某种大豆在相同条件下的发芽试验结果:
每批粒数n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
发芽的粒数m | 96 | 282 | 382 | 570 | 948 | 1904 | 2850 |
发芽的频率 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.952 | 0.950 |
下面有三个推断:
①当n为400时,发芽的大豆粒数为382,发芽的频率为0.955,所以大豆发芽的概率是0.955;
②随着试验时大豆的粒数的增加,大豆发芽的频率总在0.95附近摆动,显示出一定的稳定性,可以估计大豆发芽的概率是0.95;
③若大豆粒数n为4000,估计大豆发芽的粒数大约为3800粒.
其中推断合理的是( )
A. ①②③ B. ①② C. ①③ D. ②③