题目内容
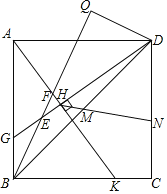
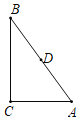
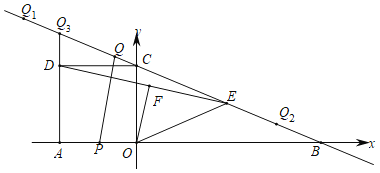
【题目】如图,在Rt△ABC中,∠C=90°,BC=2![]() ,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为_____.
,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为_____.
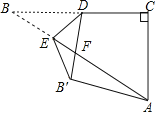
【答案】3或![]()
【解析】
由∠C=90°,BC=2![]() ,AC=2可得tanB=
,AC=2可得tanB=![]() ,即∠B=30°,再根据直角三角形的性质可得AB=2AC=4;再由翻折的性质可得DB=DC=
,即∠B=30°,再根据直角三角形的性质可得AB=2AC=4;再由翻折的性质可得DB=DC=![]() ,EB′=EB,∠DB′E=∠B=30°;设AE=x,则BE=4﹣x,EB′=4﹣x.当∠AFB′=90°时,解直角三角形可得EF=x﹣
,EB′=EB,∠DB′E=∠B=30°;设AE=x,则BE=4﹣x,EB′=4﹣x.当∠AFB′=90°时,解直角三角形可得EF=x﹣![]() ;又由在Rt△B′EF中,∠EB′F=30°,可得EB′=2EF;再用x表示出来,然后解关于x的方程即可;②当∠AB′F=90°时,即B′不落在C点处时,在进行求解即可.
;又由在Rt△B′EF中,∠EB′F=30°,可得EB′=2EF;再用x表示出来,然后解关于x的方程即可;②当∠AB′F=90°时,即B′不落在C点处时,在进行求解即可.
解:∵∠C=90°,BC=2![]() ,AC=2,
,AC=2,
∴tanB=![]() ,
,
∴∠B=30°,
∴AB=2AC=4,
∵点D是BC的中点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F
∴DB=DC=![]() ,EB′=EB,∠DB′E=∠B=30°,
,EB′=EB,∠DB′E=∠B=30°,
设AE=x,则BE=4﹣x,EB′=4﹣x,
当∠AFB′=90°时,
在Rt△BDF中,cosB=![]() ,
,
∴BF=![]() cos30°=
cos30°=![]() ,
,
∴EF=![]() ﹣(4﹣x)=x﹣
﹣(4﹣x)=x﹣![]() ,
,
在Rt△B′EF中,∵∠EB′F=30°,
∴EB′=2EF,
即4﹣x=2(x﹣![]() ),解得x=3,此时AE为3;
),解得x=3,此时AE为3;
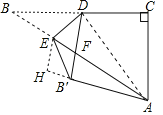
②当∠AB′F=90°时,即B′不落在C点处时,作EH⊥AB′于H,连接AD,如图,
∵DC=DB′,AD=AD,
∴Rt△ADB′≌Rt△ADC,
∴AB′=AC=2,
∵∠AB′E=∠AB′F+∠EB′F=90°+30°=120°,
∴∠EB′H=60°,
在Rt△EHB′中,B′H=![]() B′E=
B′E=![]() (4﹣x),EH=
(4﹣x),EH=![]() B′H=
B′H=![]() (4﹣x),
(4﹣x),
在Rt△AEH中,
∵EH2+AH2=AE2,
∴![]() (4﹣x)2+[
(4﹣x)2+[![]() (4﹣x)+2]2=x2,解得x=
(4﹣x)+2]2=x2,解得x=![]() ,此时AE为
,此时AE为![]() .
.
综上所述,AE的长为3或![]() .
.
故答案为3或![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】为了解某区初二年级数学学科期末质量监控情况,进行了抽样调查,过程如下,请将有关问题补充完整.
收集数据:
随机抽取甲乙两所学校的 20 名学生的数学成绩进行
甲 | 91 | 89 | 77 | 86 | 71 | 31 | 97 | 93 | 72 | 91 |
81 | 92 | 85 | 85 | 95 | 88 | 88 | 90 | 44 | 91 | |
乙 | 84 | 93 | 66 | 69 | 76 | 87 | 77 | 82 | 85 | 88 |
90 | 88 | 67 | 88 | 91 | 96 | 68 | 97 | 59 | 88 |
整理、描述数据 :
按如下数据段整理、描述这两组数据
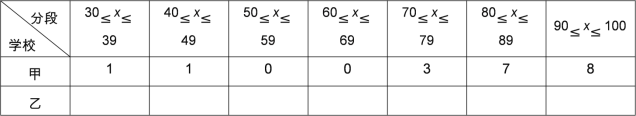
分析数据 :
两组数据的平均数、中位数、众数、方差如下表:

a经统计,表格中m的值是 ___________ .
得出结论:
b若甲学校有 400 名初二学生,估计这次考试成绩 80 分以上人数为____________ .
c可以推断出 _______学校学生的数学水平较高,理由为:①__________________;②_________________.(至少从两个不同的角度说明推断的合理性)