题目内容
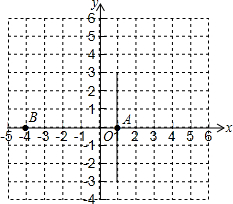平面直角坐标系xOy中，已知点A（2，0），点B（-4，0），直线l经过点A且与x轴垂直．若点B关于y轴的对称点是B1，点B1关于直线l的对称点是B2，则点B2的坐标是（-2，0）
（-2，0）
．分析：根据网格结构找出点B关于y轴的对称点B1，再找出点B1关于直线l的对称点B2的位置，然后写出坐标即可．
解答：解：如图所示，B2（-2，0）．
故答案为：（-2，0）．
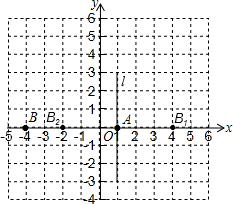
故答案为：（-2，0）．
点评：本题考查了坐标与图形变化-对称，熟练掌握数轴与网格结构，准确确定出对称点的位置是解题的关键．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
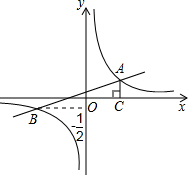如图，已知在平面直角坐标系xOy中，一次函数y=kx+b（k≠0）的图象与反比例函数y=
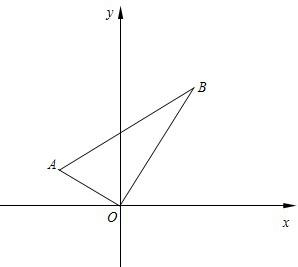90°，∠A=60°，点A的坐标为（
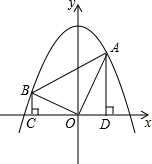A，OB，OA⊥OB，作BC⊥x轴于C点，AD⊥x轴于D点．
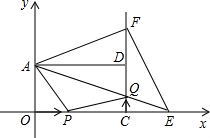（2013•河东区一模）如图，在平面直角坐标系xOy中，矩形AOCD的顶点A的坐标是（0，4），现有两动点P、Q，点P从点O出发沿线段OC（不包括端点O，C）以每秒2个单位长度的速度，匀速向点C运动，点Q从点C出发沿线段CD（不包括端点C，D）以每秒1个单位长度的速度匀速向点D运动．点P、Q同时出发，同时停止，设运动时间为t秒，当t=2秒时