题目内容
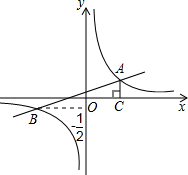 如图,已知在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=
如图,已知在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=| m |
| x |
| 1 |
| 2 |
求:(1)求反比例函数的解析式;
(2)求一次函数的解析式.
分析:(1)首先由点的坐标的意义,得出点A的坐标,然后把点A的坐标代入反比例函数的解析式y=
中,求出m的值,从而得出反比例函数的解析式;
(2)首先由点B在反比例函数y=
的图象上,可求出点B的坐标,然后根据点A、点B都在一次函数y=kx+b(k≠0)的图象上,利用待定系数法求出一次函数的解析式.
| m |
| x |
(2)首先由点B在反比例函数y=
| m |
| x |
解答:解:(1)依题意,知点A的坐标是(2,1).
∵点A在反比例函数y=
(m≠0)的图象上,
∴m=2×1=2.
∴反比例函数的解析式为y=
;
(2)∵y=
,
∴当y=-
时,x=-4.
∴点B的坐标为(-4,-
).
∵点A、点B都在一次函数y=kx+b(k≠0)的图象上,
∴
,
∴
.
∴一次函数的解析式为y=
x+
.
∵点A在反比例函数y=
| m |
| x |
∴m=2×1=2.
∴反比例函数的解析式为y=
| 2 |
| x |
(2)∵y=
| 2 |
| x |
∴当y=-
| 1 |
| 2 |
∴点B的坐标为(-4,-
| 1 |
| 2 |
∵点A、点B都在一次函数y=kx+b(k≠0)的图象上,
∴
|
∴
|
∴一次函数的解析式为y=
| 1 |
| 4 |
| 1 |
| 2 |
点评:本题主要考查了用待定系数法求函数的解析式.难度不大,此题的突破点是先由A点的坐标求出反比例函数的解析式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
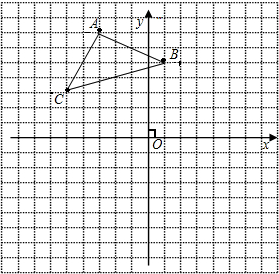 如图,已知在平面直角坐标系中,△ABC的顶点坐标为A(-3,7),
如图,已知在平面直角坐标系中,△ABC的顶点坐标为A(-3,7),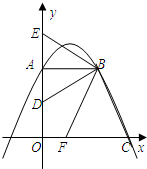 边分别交y轴的正半轴、x轴的正半轴于点E和F.
边分别交y轴的正半轴、x轴的正半轴于点E和F.
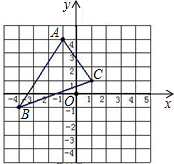 如图,已知在平面直角坐标系中,△ABC的位置如图所示
如图,已知在平面直角坐标系中,△ABC的位置如图所示