题目内容
如图,已知平面直角坐标系xOy中,点A(2,m),B(-3,n)为两动点,其中m>1,连接O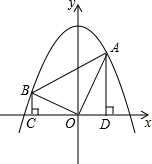 A,OB,OA⊥OB,作BC⊥x轴于C点,AD⊥x轴于D点.
A,OB,OA⊥OB,作BC⊥x轴于C点,AD⊥x轴于D点.(1)求证:mn=6;
(2)当S△AOB=10时,抛物线经过A,B两点且以y轴为对称轴,求抛物线对应的二次函数的关系式;
(3)在(2)的条件下,设直线AB交y轴于点F,过点F作直线l交抛物线于P,Q两点,问是否存在直线l,使S△POF:S△QOF=1:2?若存在,求出直线l对应的函数关系式;若不存在,请说明理由.
分析:(1)根据A、B的坐标,可得OC、OD、BC、AD的长,由于OA⊥OB,可证得△BOC∽△OAD,根据相似三角形所得比例线段,即可证得所求的结论.
(2)欲求抛物线的解析式,需先求出A、B的坐标;根据(1)的相似三角形,可得3OA=mOB,用OB表示出OA,代入△OAB的面积表达式中,可得到OB2的值,在Rt△BOC中,利用勾股定理可求得另外一个OB2的表达式,联立两式可得关于m、n的等式,结合(1)的结论即可求出m、n的值,从而确定A、B的坐标和抛物线的解析式.
(3)求直线l的解析式,需先求出P、Q的坐标,已知S△POF:S△QOF=1:2,由于两三角形同底不等高,所以面积比等于高的比,即P、Q两点横坐标绝对值的比,可设出点P的坐标,然后根据两者的比例关系表示出点Q的坐标,由于点Q在抛物线的图象上,可将其代入抛物线的解析式中,即可求得点P、Q的坐标,进而可利用待定系数法求得直线l的解析式.
(2)欲求抛物线的解析式,需先求出A、B的坐标;根据(1)的相似三角形,可得3OA=mOB,用OB表示出OA,代入△OAB的面积表达式中,可得到OB2的值,在Rt△BOC中,利用勾股定理可求得另外一个OB2的表达式,联立两式可得关于m、n的等式,结合(1)的结论即可求出m、n的值,从而确定A、B的坐标和抛物线的解析式.
(3)求直线l的解析式,需先求出P、Q的坐标,已知S△POF:S△QOF=1:2,由于两三角形同底不等高,所以面积比等于高的比,即P、Q两点横坐标绝对值的比,可设出点P的坐标,然后根据两者的比例关系表示出点Q的坐标,由于点Q在抛物线的图象上,可将其代入抛物线的解析式中,即可求得点P、Q的坐标,进而可利用待定系数法求得直线l的解析式.
解答:证明:(1)∵A,B点坐标分别为(2,m),(-3,n),
∴BC=n,OC=3,OD=2,AD=m,
又∵OA⊥OB,易证△CBO∽△DOA,
∴
=
=
,
∴
=
,
∴mn=6.
解:(2)由(1)得,OA=
BO,又S△AOB=10,
∴
OB•OA=10,
即BO•OA=20,
∴mBO2=60,
又∵OB2=BC2+OC2=n2+9,
∴m(n2+9)=60,
又∵mn=6①,
∴m(n2+9)=mn•n+9m=6n+9m=60,
∴2n+3m=20②,
∴①②联立得,m=6(m=
不合题意,舍去),n=1;
∴A坐标为(2,6),B坐标为(-3,1),
易得抛物线解析式为y=-x2+10.
(3)直线AB为y=x+4,且与y轴交于F(0,4)点,
∴OF=4,
假设存在直线l交抛物线于P,Q两点,且使S△POF:S△QOF=1:2,如图所示,
则有PF:FQ=1:2,作PM⊥y轴于M点,QN⊥y轴于N点,
∵P在抛物线y=-x2+10上,
∴设P坐标为(t,-t2+10),
则FM=-t2+10-4=-t2+6,易证△PMF∽△QNF,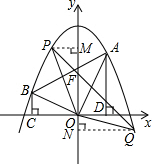
∴
=
=
=
,
∴QN=2PM=-2t,NF=2MF=-2t2+12,
∴ON=-2t2+8,
∴Q点坐标为(-2t,2t2-8),
Q点在抛物线y=-x2+10上,2t2-8=-4t2+10,
解得t=-
,(t=
舍去),
∴P坐标为(-
,7),Q坐标为(2
,-2),
∴易得直线PQ为y=-
x+4;
根据抛物线的对称性可得直线PQ的另解为y=
x+4.
∴BC=n,OC=3,OD=2,AD=m,
又∵OA⊥OB,易证△CBO∽△DOA,
∴
| CB |
| DO |
| CO |
| DA |
| BO |
| OA |
∴
| n |
| 2 |
| 3 |
| m |
∴mn=6.
解:(2)由(1)得,OA=
| m |
| 3 |
∴
| 1 |
| 2 |
即BO•OA=20,
∴mBO2=60,
又∵OB2=BC2+OC2=n2+9,
∴m(n2+9)=60,
又∵mn=6①,
∴m(n2+9)=mn•n+9m=6n+9m=60,
∴2n+3m=20②,
∴①②联立得,m=6(m=
| 2 |
| 3 |
∴A坐标为(2,6),B坐标为(-3,1),
易得抛物线解析式为y=-x2+10.
(3)直线AB为y=x+4,且与y轴交于F(0,4)点,
∴OF=4,
假设存在直线l交抛物线于P,Q两点,且使S△POF:S△QOF=1:2,如图所示,
则有PF:FQ=1:2,作PM⊥y轴于M点,QN⊥y轴于N点,
∵P在抛物线y=-x2+10上,
∴设P坐标为(t,-t2+10),
则FM=-t2+10-4=-t2+6,易证△PMF∽△QNF,

∴
| PM |
| QN |
| MF |
| FN |
| PF |
| QF |
| 1 |
| 2 |
∴QN=2PM=-2t,NF=2MF=-2t2+12,
∴ON=-2t2+8,
∴Q点坐标为(-2t,2t2-8),
Q点在抛物线y=-x2+10上,2t2-8=-4t2+10,
解得t=-
| 3 |
| 3 |
∴P坐标为(-
| 3 |
| 3 |
∴易得直线PQ为y=-
| 3 |
根据抛物线的对称性可得直线PQ的另解为y=
| 3 |
点评:此题主要考查了相似三角形的判定和性质、勾股定理、图形面积的求法以及用待定系数法确定函数解析式的方法,在(3)题中,能够将三角形的面积比转化为P、Q两点横坐标的比例关系是解决问题的关键.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 的图象与y轴交于点A,
的图象与y轴交于点A, 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐 时x的取值范围。
时x的取值范围。
 中,四边形OABC是矩形,点A,C的坐
中,四边形OABC是矩形,点A,C的坐 =-
=- +
+ 交折线O-A-B于点E.
交折线O-A-B于点E.
