题目内容
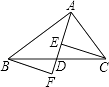
【题目】如图，AC=AB，DC=DB，AD与BC相交于O． 
（1）求证：△ACD≌△ABD；
（2）求证：AD垂直平分BC．
【答案】
（1）证明：在△ADC和△ADB中，
，
∴△ACD≌△ABD．
（2）证明：方法一∵△ACD≌△ABD
∴∠BAO=∠CAO
又∵AB=AC，
∴△ABC为等腰三角形，
∴AO⊥BC、CO=BO，
∴AD垂直平分BC．
方法二∵AB=AC，
∴点A在BC的垂直平分线上，
∵DC=DB，
∴点D在BC的垂直平分线上，
∴AD垂直平分BC．
【解析】（1）根据SSS即可证明．（2）根据线段垂直平分线的定义即可证明．
【考点精析】通过灵活运用线段垂直平分线的性质，掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等即可以解答此题．
练习册系列答案
相关题目
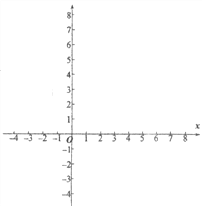
【题目】有这样一个问题：探究函数y=
的图象与性质。小慧根据学习函数的经验，对函数y=
的图象与性质进行了探究。下面是小慧的探究过程，请补充完成：
（1）函数y=
的自变量x的取值范围是__________；
（2）列出y与x的几组对应值。请直接写出m的值，m=________；
x | … | -3 | -2 | 0 | 1 | 1.5 | 2.5 | m | 4 | 6 | 7 | … |
y | … | 2.4 | 2.5 | 3 | 4 | 6 | -2 | 0 | 1 | 1.5 | 1.6 | … |
（3）请在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点，并画出该函数的图象；
（4）结合函数的图象，写出该函数的两条性质：
①_____________________________________________；
②____________________________________________。
