��Ŀ����
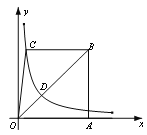
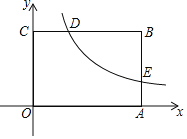
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�����OABC�Ķ���A��x����������ϣ�����C��y����������ϣ�D��BC���ϵ�һ�㣬OC��CD��5��3��DB��6������������y��![]() ��k��0���ڵ�һ�����ڵ�ͼ����D����AB�ڵ�E��AE��BE��1��2��
��k��0���ڵ�һ�����ڵ�ͼ����D����AB�ڵ�E��AE��BE��1��2��
��1������������������ı���ʽ��
��2������P�ھ���OABC�ڣ�������S��PAO��![]() S�ı���OABC��
S�ı���OABC��
������P�����������������ͼ���ϣ����P�����ꣻ
������Q��ƽ����һ��ʹ����A��B��P��QΪ������ı������������Q�����꣮
���𰸡���1��y��![]() ����2���٣�
����2���٣�![]() ��4�����ڣ�6��9����9��2
��4�����ڣ�6��9����9��2![]() ����1����
����1����
��������
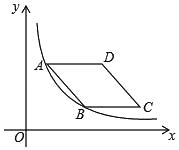
��1�����B������Ϊ��m��n�������E������Ϊ��m��![]() n������D������Ϊ��m��6��n�������÷���������ͼ���ϵĵ���������������m��ֵ��֮���һ�����n��ֵ��Ȼ���һ����⼴�ɣ�
n������D������Ϊ��m��6��n�������÷���������ͼ���ϵĵ���������������m��ֵ��֮���һ�����n��ֵ��Ȼ���һ����⼴�ɣ�
��2�����������ε������ʽ����ε������ʽ���S��PAO��![]() S�ı���OABC���ɽ�һ�����P��������.������P�����������������ͼ���ϣ����÷���������ͼ���ϵ�����������������P�����ꣻ���ɵ�A��B�����꼰��P��������ɵó�AP��BP�������ɵó�AB����Ϊ�Խ��ߣ����P������Ϊ��t��4������AP��AB��BP��AB����������ǣ���i����AB��APʱ�����������ľ��빫ʽ�����tֵ�������ɵó���P1�����꣬���P1Q1�ij��������Q1�����ꣻ��ii����BP��ABʱ�����������ľ��빫ʽ�����tֵ�������ɵó���P2�����꣬���P2Q2�ij��������Q2�����꣮
S�ı���OABC���ɽ�һ�����P��������.������P�����������������ͼ���ϣ����÷���������ͼ���ϵ�����������������P�����ꣻ���ɵ�A��B�����꼰��P��������ɵó�AP��BP�������ɵó�AB����Ϊ�Խ��ߣ����P������Ϊ��t��4������AP��AB��BP��AB����������ǣ���i����AB��APʱ�����������ľ��빫ʽ�����tֵ�������ɵó���P1�����꣬���P1Q1�ij��������Q1�����ꣻ��ii����BP��ABʱ�����������ľ��빫ʽ�����tֵ�������ɵó���P2�����꣬���P2Q2�ij��������Q2�����꣮
��1�����B��������m��n�������E��������m��![]() n������D��������m��6��n����
n������D��������m��6��n����
�ߵ�D��E�ڷ���������y��![]() ��k��0����ͼ���ϣ�
��k��0����ͼ���ϣ�
��k��![]() mn����m��6��n��
mn����m��6��n��
��m��9��
��OC��CD��5��3��
��n����m��6����5��3��
��n��5��
��k��![]() mn��
mn��![]() ��9��5��15��
��9��5��15��
�෴���������ı���ʽΪy��![]() ��
��
��2����S��PAO��![]() S�ı���OABC��
S�ı���OABC��
��![]() OAyP��
OAyP��![]() OAOC��
OAOC��
��yP��![]() OC��4��
OC��4��
��y��4ʱ��![]() ��4��
��4��
��ã�x��![]() ��
��
������P�����������������ͼ���ϣ���P������Ϊ��![]() ��4����
��4����
���ɣ�1����֪����A������Ϊ��9��0������B������Ϊ��9��5����
��yP��4��yA+yB��5��
��![]() ��
��
��AP��BP��
��AB����Ϊ�Խ��ߣ�
���P��������t��4����
��AP��AB��BP��AB����������ǣ���ͼ��ʾ����
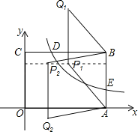
��i����AB��APʱ����9��t��2+��4��0��2��52��
��ã�t1��6��t2��12����ȥ����
���P1��������6��4����
�֡�P1Q1��AB��5��
���Q1��������6��9����
��ii����BP��ABʱ����9��t��2+��5��4��2��52��
��ã�t3��9��2![]() ��t4��9+2
��t4��9+2![]() ����ȥ����
����ȥ����
���P2��������9��2![]() ��4����
��4����
�֡�P2Q2��AB��5��
���Q2��������9��2![]() ����1����
����1����
������������Q��������6��9����9��2![]() ����1����
����1����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�