题目内容
如图1所示,在等腰Rt△ABC中,点M是斜边AB中点,D是AB边上一动点,ED⊥CD于点D,EF⊥AB交AB于点F,且CD=ED.
(1)求证:AC=
DF;
(2)如图2所示,若ED⊥CD于点D,且ED=CD,点E在AC的左侧,其它条件不变,连接AE,求证:AE∥BC;
(3)在(2)中,若AD=
,则BC-AE=
.(直接写出结果即可,不书写解答过程)

(1)求证:AC=
| 2 |
(2)如图2所示,若ED⊥CD于点D,且ED=CD,点E在AC的左侧,其它条件不变,连接AE,求证:AE∥BC;
(3)在(2)中,若AD=
| 3 |
| 6 |
| 6 |

分析:(1)连接CM,求出△DCM≌△EDF,推出DF=CM,根据勾股定理求出即可.
(2)过E作EF⊥AB交BA延长线于F,根据△DCM≌△EDF,推出EF=DM,DF=CM,CM=AM,求出DF=AM,求出AF=EF,求出∠FAE=∠B即可.
(3)过E作EN∥AB交BC于N,交CM于Q,求出BC-AE=CN,求出四边形AENB是平行四边形,四边形FEQM是矩形,求出AD=CQ=
,求出CQ=QN=
,在Rt△CQN中,由勾股定理求出CN即可.
(2)过E作EF⊥AB交BA延长线于F,根据△DCM≌△EDF,推出EF=DM,DF=CM,CM=AM,求出DF=AM,求出AF=EF,求出∠FAE=∠B即可.
(3)过E作EN∥AB交BC于N,交CM于Q,求出BC-AE=CN,求出四边形AENB是平行四边形,四边形FEQM是矩形,求出AD=CQ=
| 3 |
| 3 |
解答:(1)证明: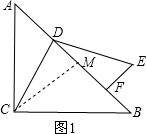
连接CM,
∵△ACB是等腰直角三角形,M为AB中点,
∴AM=CM=BM,CM⊥AB,
∵EF⊥AB,CD⊥DE,
∴∠CMD=∠DFE=∠CDE=90°,
∴∠CDM+∠EDF=90°,∠CDM+∠DCM=90°,
∴∠DCM=∠EDF,
在△DCM和△EDF中
∴△DCM≌△EDF(AAS),
∴DF=CM,
∵△ACB中,∠ACB=90°,AC=BC,
∴∠A=∠B=45°,
∵∠CMA=90°,AM=CM,由勾股定理得:AC=
CM,
∴AC=
DF.
(2)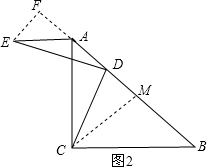
证明:过E作EF⊥AB交BA延长线于F,
∵由(1)知:△DCM≌△EDF,
∴EF=DM,DF=CM,CM=AM,
∴DF=AM,
∴DF-AD=AM-AD,
∴AF=DM,
∴AF=EF,
∵∠F=90°,
∴∠FAE=∠FEA=45°,
∵∠B=45°,
∴∠FAE=∠B,
∴AE∥BC.
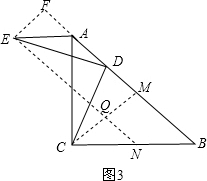
(3)解:BC-AE=
,
理由是:过E作EN∥AB交BC于N,交CM于Q,如图3,
∵AE∥BC,
∴四边形AENB是平行四边形,
∴AE=BN,
∴BC-AE=CN,
∵EF⊥AB,CM⊥AB,
∴CM∥EF,∠QMF=90°,
∵EQ∥AB,
∴四边形FEQM是矩形,
∴∠EQM=∠CQM=90°,EF=QM,
∵DM=EF,
∴QM=DM,
∵AM=CM,
∴AD=CQ=
,
∵∠ACB=90°,AC=BC,M为AB中点,
∴∠MCB=45°,
∴∠QNC=45°=∠QCN,
∴CQ=QN=
,
在Rt△CQN中,由勾股定理得:CN=
=
,
即BC-AE=
,
故答案为:
.

连接CM,
∵△ACB是等腰直角三角形,M为AB中点,
∴AM=CM=BM,CM⊥AB,
∵EF⊥AB,CD⊥DE,
∴∠CMD=∠DFE=∠CDE=90°,
∴∠CDM+∠EDF=90°,∠CDM+∠DCM=90°,
∴∠DCM=∠EDF,
在△DCM和△EDF中
|
∴△DCM≌△EDF(AAS),
∴DF=CM,
∵△ACB中,∠ACB=90°,AC=BC,
∴∠A=∠B=45°,
∵∠CMA=90°,AM=CM,由勾股定理得:AC=
| 2 |
∴AC=
| 2 |
(2)

证明:过E作EF⊥AB交BA延长线于F,
∵由(1)知:△DCM≌△EDF,
∴EF=DM,DF=CM,CM=AM,
∴DF=AM,
∴DF-AD=AM-AD,
∴AF=DM,
∴AF=EF,
∵∠F=90°,
∴∠FAE=∠FEA=45°,
∵∠B=45°,
∴∠FAE=∠B,
∴AE∥BC.

(3)解:BC-AE=
| 6 |
理由是:过E作EN∥AB交BC于N,交CM于Q,如图3,
∵AE∥BC,
∴四边形AENB是平行四边形,
∴AE=BN,
∴BC-AE=CN,
∵EF⊥AB,CM⊥AB,
∴CM∥EF,∠QMF=90°,
∵EQ∥AB,
∴四边形FEQM是矩形,
∴∠EQM=∠CQM=90°,EF=QM,
∵DM=EF,
∴QM=DM,
∵AM=CM,
∴AD=CQ=
| 3 |
∵∠ACB=90°,AC=BC,M为AB中点,
∴∠MCB=45°,
∴∠QNC=45°=∠QCN,
∴CQ=QN=
| 3 |
在Rt△CQN中,由勾股定理得:CN=
(
|
| 6 |
即BC-AE=
| 6 |
故答案为:
| 6 |
点评:本题考查了矩形的性质和判定,等腰直角三角形性质,勾股定理,全等三角形的性质和判定的应用,主要考查学生综合运用性质进行推理的能力.有一定的难度.

练习册系列答案
相关题目