题目内容
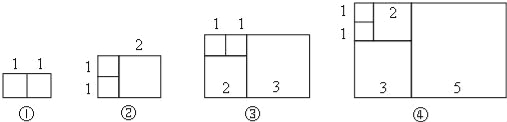
【题目】如图,将边长分别为1、2、3、5、…的若干正方形按一定的规律拼成不同的矩形,依次记作矩形①、矩形②、矩形③、矩形④,那么按此规律.
(1)组成第n个矩形的正方形的个数为 个;
(2)求矩形⑥的周长.
【答案】(1)(n+1)个(2)68
【解析】
试题分析:(1)由矩形①、②、③中正方形个数即可得知;结合图形分析,①的周长为:2(1+2),②的周长为:2(2+3),③的周长为:2(3+5),④的周长为:2(5+8),由此可推出第n个长方形的宽为第n﹣1个长方形的长,第n个长方形的长为第n﹣1个长方形的长和宽的和,据此可得.
试题解析:(1)∵矩形①中,正方形个数为1;矩形②中,正方形个数为3;矩形③中,正方形个数为4;…,
∴组成第n个矩形的正方形的个数为(n+1)个;
(2)∵①的周长为:2(1+2),
②的周长为:2(2+3),
③的周长为:2(3+5),
④的周长为:2(5+8),
由此可推出第n个长方形的宽为第n﹣1个长方形的长,
第n个长方形的长为第n﹣1个长方形的长和宽的和.
可得:第⑤个的周长为:2(8+13),
第⑥的周长为:2(13+21)=68;

练习册系列答案
相关题目