题目内容
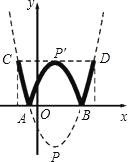
【题目】已知：如图，抛物线y=a（x﹣1）2+c与x轴交于点A（
，0）和点B，将抛物线沿x轴向上翻折，顶点P落在点P′（1，3）处．
（1）求原抛物线的解析式；
（2）学校举行班徽设计比赛，九年级5班的小明在解答此题时顿生灵感：过点P′作x轴的平行线交抛物线于C、D两点，将翻折后得到的新图象在直线CD以上的部分去掉，设计成一个“W”型的班徽，“5”的拼音开头字母为W，“W”图案似大鹏展翅，寓意深远；而且小明通过计算惊奇的发现这个“W”图案的高与宽（CD）的比非常接近黄金分割比
（约等于0.618）．请你计算这个“W”图案的高与宽的比到底是多少？（参考数据：
，
，结果可保留根号）
【答案】（1）y=x2﹣2x﹣2（2）0.6124
【解析】
试题分析：（1）利用P与P′（1，3）关于x轴对称，得出P点坐标，利用待定系数法求出二次函数的解析式即可；
（2）根据已知得出C，D两点坐标，进而得出“W”图案的高与宽（CD）的比．
试题解析：（1）∵P与P′（1，3）关于x轴对称，
∴P点坐标为（1，﹣3）；
∵抛物线y=a（x﹣1）2+c过点A（
，0），顶点是P（1，﹣3），
∴
；
解得
；
则抛物线的解析式为y=（x﹣1）2﹣3，…
即y=x2﹣2x﹣2．
（2）∵CD平行x轴，P′（1，3）在CD上，
∴C、D两点纵坐标为3；
由（x﹣1）2﹣3=3，
解得：
，
∴C、D两点的坐标分别为（
，3），（
，3）
∴CD=
∴“W”图案的高与宽（CD）的比=
（或约等于0.6124）．
名校课堂系列答案
【题目】为了打造区域中心城市，实现攀枝花跨越式发展，我市花城新区建设正按投资计划有序推进．花城新区建设工程部，因道路建设需要开挖土石方，计划每小时挖掘土石方540m3 ， 现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作，租赁公司提供的挖掘机有关信息如下表所示：
租金（单位：元/台时） | 挖掘土石方量（单位：m3/台时） | |
甲型挖掘机 | 100 | 60 |
乙型挖掘机 | 120 | 80 |
（1）若租用甲、乙两种型号的挖掘机共8台，恰好完成每小时的挖掘量，则甲、乙两种型号的挖掘机各需多少台？
（2）如果每小时支付的租金不超过850元，又恰好完成每小时的挖掘量，那么共有哪几种不同的租用方案？
