题目内容
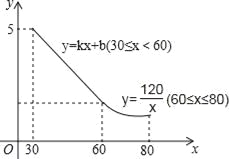
【题目】某工艺品厂生产一种汽车装饰品,每件生产成本为20元,销售价格在30元至80元之间(含30元和80元),销售过程中的管理、仓储、运输等各种费用(不含生产成本)总计50万元,其销售量y(万个)与销售价格(元/个)的函数关系如图所示.
(1)当30≤x≤60时,求y与x的函数关系式;
(2)求出该厂生产销售这种产品的纯利润w(万元)与销售价格x(元/个)的函数关系式;
(3)销售价格应定为多少元时,获得利润最大,最大利润是多少?
【答案】(1)y=﹣0.1x+8(30≤x≤60)(2)w=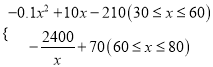 (3)当销售价格定为50元/件或80元/件,获得利润最大,最大利润是40万元
(3)当销售价格定为50元/件或80元/件,获得利润最大,最大利润是40万元
【解析】试题分析:(1)由图象知,当30≤x≤60时,图象过(60,2)和(30,5),运用待定系数法求解析式即可;
(2)根据销售产品的纯利润=销售量×单个利润,分30≤x≤60和60<x≤80列函数表达式;
(3)当30≤x≤60时,运用二次函数性质解决,当60<x≤80时,运用反比例函数性质解答.
试题解析:(1)当x=60时,y=![]() =2,
=2,
∴当30≤x≤60时,图象过(60,2)和(30,5),
设y=kx+b,则![]() ,
,
解得: ![]() ,
,
∴y=﹣0.1x+8(30≤x≤60);
(2)根据题意,当30≤x≤60时,W=(x﹣20)y﹣50=(x﹣20)(﹣0.1x+8)﹣50=![]() +10x﹣210,
+10x﹣210,
当60<x≤80时,W=(x﹣20)y﹣50=(x﹣20)![]() ﹣50=
﹣50=![]() +70,
+70,
综上所述:W=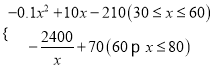 ;
;
(3)当30≤x≤60时,W=![]() +10x﹣210=
+10x﹣210=![]() ,
,
当x=50时, ![]() =40(万元);
=40(万元);
当60<x≤80时,W=![]() +70,
+70,
∵﹣2400<0,W随x的增大而增大,
∴当x=80时, ![]() =
=![]() +70=40(万元),
+70=40(万元),
答:当销售价格定为50元/件或80元/件,获得利润最大,最大利润是40万元.