题目内容
【题目】如图，抛物线y＝
+bx+c经过△ABC的三个顶点，其中点A（0，﹣1），点B（9，﹣10），AC∥x轴，点P是直线AC上方抛物线上的动点．
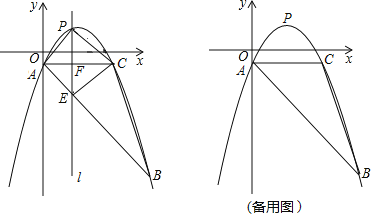
（1）求抛物线的解析式；
（2）过点P且与y轴平行的直线l与直线AB，AC分别交于点E，F，当四边形AECP的面积最大时，求点P的坐标；
（3）当点P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C，P，Q为顶点的三角形与△ABC相似？若存在，求出点Q的坐标；若不存在，请说明理由．
【答案】（1）
；（2）
，
；（3）
或
．
【解析】
（1）根据待定系数法，可得函数解析式；
（2）根据平行于
轴的直线上点的纵坐标相等，可得
点的纵坐标，根据自变量与函数值的对应关系，可得点坐标，根据待定系数法，可得
的解析式，根据直线上的点满足函数解析式，可得
点坐标，根据平行于
轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标，可得
的长，根据面积的和差，可得二次函数，根据二次函数的性质，可得答案；
（3）根据等腰直角三角形的性质，可得
，根据相似三角形的判定，可得关于
的方程，根据解方程，可得答案．
解：（1）将
，
代入函数解析式，得
，
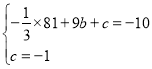解得
，
抛物线的解析式；
（2）
轴，，
．
解得
，
．
点的坐标为
．
点，，
直线的解析式为
．
设点
，
．
．
，
，
．
，
当
时，四边形
的面积的最大值是
．
此时点，．
（3）
，
．
，
．
．
．
同理可得
．
．
分两种情况：如图，
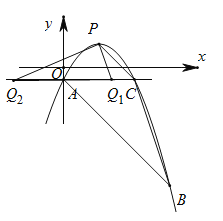
①当
时，
．
，，
，
．
解得
．
．
②当
时，
．即
．
解得
．
．
综合①②得，存在这样的点
，其坐标是或．
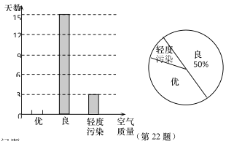
【题目】我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动，为了解学生对四种项目的喜欢情况，随机调查了该校m名学生最喜欢的一种项目（每名学生必选且只能选择四种活动项目的一种），并将调查结果绘制成如下的不完整的统计图表：
学生最喜欢的活动项目的人数统计表
项目 | 学生数（名） | 百分比 |
丢沙包 | 20 | 10% |
打篮球 | 60 | p% |
跳大绳 | n | 40% |
踢毽球 | 40 | 20% |
根据图表中提供的信息，解答下列问题：
（1）m= ，n= ，p= ；
（2）请根据以上信息直接补全条形统计图；
（3）根据抽样调查结果，请你估计该校2000名学生中有多少名学生最喜欢跳大绳．
【题目】为了掌握八年级数学考试卷的命题质量与难度系数，命题组教师赴外地选取一个水平相当的八年级班级进行预测，将考试成绩分布情况进行处理分析，制成如图表（成绩得分均为整数）：
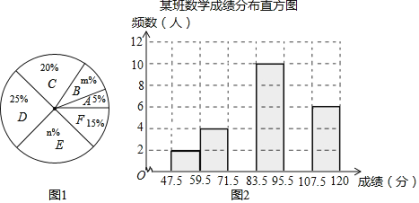
根据图表中提供的信息解答下列问题：
组别 | 成绩分组 | 频数 |
A | 47.5～59.5 | 2 |
B | 59.5～71.5 | 4 |
C | 71.5～83.5 | a |
D | 83.5～95.5 | 10 |
E | 95.5～107.5 | b |
F | 107.5～120 | 6 |
（1）频数分布表中的a＝ ，b＝ ；扇形统计图中的m＝ ，n＝ ；
（2）已知全区八年级共有200个班（平均每班40人），用这份试卷检测，108分及以上为优秀，预计优秀的人数约为 人，72分及以上为及格，预计及格的人数约为 人；
（3）补充完整频数分布直方图．
【题目】在新冠疫情防控期间，某医疗器械商业集团新进了40台A型电子体温测量仪，60台B型电子体温测量仪，计划调配给下属的甲、乙两个连锁店销售，其中70台给甲连锁店，30台给乙连锁店．两个连锁店销售这两种测量仪每台的利润(元)如下表：
A型 | B型 | |
甲连锁店 | 200 | 170 |
乙连锁店 | 160 | 150 |
设集团调配给甲连锁店
台A型测量仪，集团卖出这100台测量仪的总利润为
(元)．
（1）求关于的函数关系式，并求出的取值范围：
（2）为了促销，集团决定仅对甲连锁店的A型测量仪每台让利
元销售，其他的销售利润不变，并且让利后每台A型测量仪的利润仍然高于甲连锁店销售的每台B型测量仪的利润，问该集团应该如何设计调配方案，使总利润达到最大?
