Question

【题目】任画一个直角三角形，分别以它的三条边为边向外做等边三角形，
要求：
（1）画出图形；
（2）探究这三个等边三角形面积之间的关系，并说明理由.

Answer 1

【答案】
（1）解：如图所示：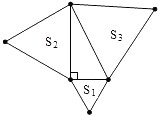

（2）解：设直角三角形的三边从小到大是a，b，c

又
则 .即斜边所在等边三角形的面积是另外两个等边三角形面积之和
【解析】（1）根据边边边定理用尺规作图即可。
（2）设直角三角形的三边从小到大是a，b，c，因为等边三角形的高=a，则面积=aa，通过计算并由勾股定理可得+ = ,即斜边所在等边三角形的面积是另外两个等边三角形面积之和.
【考点精析】解答此题的关键在于理解三角形的面积的相关知识，掌握三角形的面积=1/2×底×高，以及对勾股定理的概念的理解，了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．