题目内容
【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC与点E、F,垂足为O.
(1)如图(1),连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图(2),动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周,即点P自A→F→B→A停止,点Q自C→D→E→C停止,在运动过程中,已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
【答案】
(1)证明:证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EAO=∠FCO,
∵AC的垂直平分线EF,
∴OA=OC,
在△AOE和△COF中,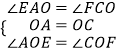 ,
,
∴△AOE≌△COF(ASA),
∴OE=OF,
∵OA=OC,
∴四边形AFCE是平行四边形,
∵EF⊥AC,
∴四边形AFCE是菱形.
∴AF=FC,
设AF=xcm,
则CF=xcm,BF=(8﹣x)cm,
∵四边形ABCD是矩形,
∴∠B=90°,
∴在Rt△ABF中,
由勾股定理得:42+(8﹣x)2=x2 ,
解得x=5,即AF=5cm
(2)解:显然当P点在AF上时,Q点在CD上,此时A、C、P、Q四点不可能构成平行四边形;
同理P点在AB上时,Q点在DE或CE上或P在BF,Q在CD时不构成平行四边形,也不能构成平行四边形.
因此只有当P点在BF上、Q点在ED上时,才能构成平行四边形,
如图所示: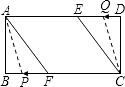
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,PC=QA,
∵点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,
∴PC=5t,QA=12﹣4t,
∴5t=12﹣4t,
解得t= ![]() .
.
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,t= ![]() 秒.
秒.
【解析】(1)根据矩形的性质及垂直平分线的性质得出∠EAO=∠FCO,OA=OC,再证明△AOE≌△COF,得出OE=OF,再根据EF⊥AC,可证得四边形AFCE是菱形.由菱形的性质得出AF=CF,然后在Rt△ABF中,设未知数,根据勾股定理建立方程求解即可得出AF的长。
(2)根据已知结合图形,分情况讨论:可知当P点在AF上时,Q点在CD上或P点在AB上时,Q点在DE或CE上或P在BF,Q在CD时,以A、C、P、Q四点为顶点不能构造平行四边形;只有当P点在BF上、Q点在ED上时,才能构成平行四边形,得出PC=QA,建立关于t的方程求解即可。
【考点精析】关于本题考查的勾股定理的概念和平行四边形的性质,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能得出正确答案.

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案