题目内容
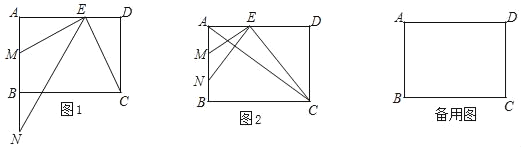
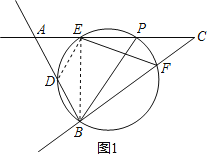
【题目】如图,在锐角△ABC中,BC=10,AC=11,△ABC的面积为33,点P是射线CA上一动点,以BP为直径作圆交线段AC于点E,交射线BA于点D,交射线CB于点F.
(1)当点P在线段AC上时,若点E为![]() 中点,求BP的长.
中点,求BP的长.
(2)连结EF,若△CEF为等腰三角形,求所有满足条件的BP值.
(3)将DE绕点D顺时针旋转90°,当点E的对应点E'恰好落在BC上时,记△DBE'的面积为S1,△DPE的面积S2,则![]() 的值为 .(直接写出答案即可)
的值为 .(直接写出答案即可)
【答案】(1)![]() ;(2)
;(2)![]() 或10或2
或10或2![]() ;(3)
;(3)![]() .
.
【解析】
(1)先利用面积求高BE,再由勾股定理求AB、AE、CE,再根据全等三角形判定和性质求得PB;
(2)△CEF为等腰三角形,可以分三种情况:①CF=EF,过F作FG⊥AC于点G,连接PF,利用相似三角形性质即可得到答案;②EF=CE,过E作EG⊥CB于G,连接EF、BP,利用全等三角形判定和性质即可;③CE=CF,利用全等三角形判定、性质和勾股定理即可;
(3)过点E作EM⊥DP于点M,过E′作E′G⊥AC于点G,作E′N⊥AB于点N,过D作DF⊥AC于点F,作DH⊥E′G于点H,依次证明:DFGH是矩形,△DEF≌△DE′H(AAS),△E′DN≌△EDM(AAS),再运用由相似三角形性质和解直角三角形知识即可.
解:(1)如图1,连接BE、DE,∴BP为直径,
∴∠BEC=∠BEA=90°
∵BC=10,AC=11,△ABC的面积为33,
∴![]() ACBE=33
ACBE=33
∴BE=6
∴CE=![]() =8
=8
∴AE=AC﹣CE=3
∴AB=![]() =3
=3![]()
∵点E为![]() 中点
中点
∴∠ABE=∠PBE
∵BE=BE
∴△ABE≌△PBE(ASA)
∴BP=AB=3![]() ;
;
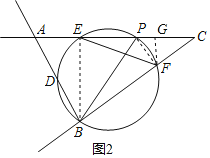
(2)∵△CEF为等腰三角形,可以分三种情况:
①CF=EF,如图2,过F作FG⊥AC于点G,连接PF,
∵BP是直径
∴∠BFP=∠CFP=∠CGF=∠CEB=90°
∴EG=CG=![]() CF=4
CF=4
∵FG∥BE
∴△CFG∽△CBE∽△CPF
∴![]() =
=![]() =
=![]() ,
,![]() =
=![]()
∴![]() ,即CF=5,
,即CF=5,
∴![]() =
=![]() ,即CP=
,即CP=![]() ,
,
∴EP=CE﹣CP=8﹣![]() =
=![]() ,
,
∴BP=![]() =
=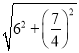 =
=![]() ;
;
②EF=CE,如图3,过E作EG⊥CB于G,连接EF、BP,则CG=GF
∴∠EFG=∠C
∵![]() =
=![]()
∴∠BPE=∠EFG
∴∠C=∠BPE
∵∠CEB=∠PEB=90°,BE=BE
∴△CBE≌△PBE(AAS)
∴BP=BC=10
③CE=CF,如图4,连接EF、BP、BE、AF,
∵BP为直径
∴∠AFB=∠AEB=90°
∵∠C=∠C
∴△CEB≌△CFP(ASA)
∴CP=CB=10
∴PE=2
∴BP=![]() =
=![]() =2
=2![]()
综上所述,满足条件的BP值为:![]() 或10或
或10或![]() .
.
(3)如图5,过点E作EM⊥DP于点M,过E′作E′G⊥AC于点G,作E′N⊥AB于点N,过D作DF⊥AC于点F,作DH⊥E′G于点H,
∵DF⊥AC,DH⊥E′G,E′G⊥AC
∴∠DFE=∠DHE′=∠E′GF=90°
∴DFGH是矩形,
∴GH=DF FG=DH∠FDH=90°
∴∠EDF+∠EDH=90°
∵∠EDH+∠E′DH=90°
∴∠EDF=∠E′DH
∵DE=DE′
∴△DEF≌△DE′H(AAS)
∴DF=DH,EF=E′H
∵DF∥BE
∴![]() =
=![]() =
=![]() ,设AF=m,则:DF=DH=GH=FG=2m,EF=E′H=3﹣m,
,设AF=m,则:DF=DH=GH=FG=2m,EF=E′H=3﹣m,
∴E′G=m+3,AG=3m,CG=CA﹣AG=11﹣3m,
∵tan∠C=![]() =
=![]() =
=![]() =
=![]() ,即:4E′G=3CG,
,即:4E′G=3CG,
∴4(m+3)=3(11﹣3m),解得:m=![]() ,
,
EF=3﹣![]() =
=![]() ,DF=2×
,DF=2×![]() =
=![]() ,
,
∵BP是直径,
∴∠E′DN+∠E′DP=90°,
∵∠E′DP+∠EDM=90°
∴∠E′DN=∠EDM
∴△E′DN≌△EDM(AAS)
∴E′N=EM
∴![]() =
=![]() =
=![]() =tan∠BPD
=tan∠BPD
∵![]()
∴∠BED=∠BPD
∵DF∥BE
∴∠BED=∠EDF
∴∠BPD=∠EDF
∴tan∠BPD=tan∠EDF=![]() =
=![]()
∴![]() =
=![]() ,
,
故答案为:![]() .
.




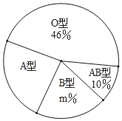
【题目】“只要人人献出一点爱,世界将变成美好的人间”.某大学利用“世界献血日”开展自愿义务献血活动,经过检测,献血者血型有“A、B、AB、O”四种类型,随机抽取部分献血结果进行统计,根据结果制作了如图两幅不完整统计图表(表,图):
血型统计表
血型 | A | B | AB | O |
人数 |
| 10 | 5 |
|
(1)本次随机抽取献血者人数为 人,图中m= ;
(2)补全表中的数据;
(3)若这次活动中该校有1300人义务献血,估计大约有多少人是A型血?
(4)现有4个自愿献血者,2人为O型,1人为A型,1人为B型,若在4人中随机挑选2人,利用树状图或列表法求两人血型均为O型的概率.