题目内容
【题目】已知:在△ABC中,D为BC边上一点,B,C两点到直线AD的距离相等.
(1)如图1,若△ABC是等腰三角形,AB=AC,则点D的位置在;
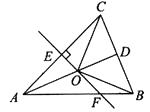
(2)如图2,若△ABC是任意一个锐角三角形,猜想点D的位置是否发生变化,请补全图形并加以证明;
(3)如图3,当△ABC是直角三角形,∠A=90°,并且点D满足(2)的位置条件,用等式表示线段AB,AC,AD之间的数量关系并加以证明.
【答案】
(1)点D为线段BC的中点
(2)证明:如图1,作BE⊥AD于点E,CF⊥AD于点F,

∵BE⊥AD于点E,CF⊥AD于点F,
∴∠3=∠4=90°,
在△BED和△CFD中,
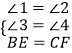
∴△BED≌△CFD.
∴BD=DC.即点D是BC边的中点.
(3)证明:如图2,延长AD到点H使DH=AD,连接HC.
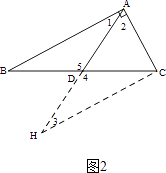
∵点D是BC边的中点,
∴BD=DC.
在△ABD和△HCD中,

∴△ABD≌△HCD.
∴∠1=∠3,AB=CH.
∵∠A=90°,
∴∠1+∠2=90°.
∴∠2+∠3=90°.
∴∠ACH=90°.
∴AC2+CH2=AH2.
又∵DH=AD,
∴AC2+AB2=(2AD)2.
∴AC2+AB2=4AD2.
【解析】(1)根据等腰三角形底边上的三线合一知D点在BC的中点处;
(2)作BE⊥AD于点E,CF⊥AD于点F,根据垂直的定义得出∠3=∠4=90°,然后利用AAS判断出△BED≌△CFD.根据全等三角形对应边相等得出BD=DC.即点D是BC边的中点;
(3)延长AD到点H使DH=AD,连接HC.根据中点定义得BD=DC,然后由SAS判断出△ABD≌△HCD,根据全等三角形的性质得∠1=∠3,AB=CH.然后根据等量代换得出∠ACH=90°.根据够勾股定理得出AC2+CH2=AH2.又因DH=AD,故AC2+AB2=(2AD)2,即AC2+AB2=4AD2.