Question

【题目】如图，在△ABC中，BD平分∠ABC，

（1）作图：作BC边的垂直平分线分别交BC，BD于点E，F（用尺规作图法，保留作图痕迹，不要求写作法）；
（2）在（1）的条件下，连接CF，若∠A=60°，∠ABD=24°，求∠ACF的度数.

Answer 1

【答案】
（1）解：如图：

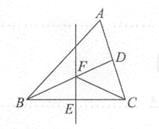
（2）解：∵ BD平分∠ABC，∠ABD=24°，

∴ ∠FBC=24°

∵ EF垂直平分BC，

∴ BF=CF

∴ ∠FCB=∠FBC=24°

在△FDC中，∠FDC=∠A+∠ABD=60°+24°=84°

∠DFC=∠FCB+∠FBC=24°+24°=48°

∴ ∠ACF=180°-84°-48°=48°

【解析】（1）分别以点B,C为圆心，大于BC的长度为半径，画弧，两弧在BC的两侧都相交，，过两弧的交点画直线，交BD于点F，交BC于点E ,则EF就是所求BC边的垂直平分线的；
（2）根据角平分线的定义得出 ∠FBC=24°，根据垂直平分线的性质的出BF=CF，根据等边对等角得出 ∠FCB=∠FBC=24°，根据三角形的外角的性质得出∠FDC=∠A+∠ABD=60°+24°=84°，FC=∠FCB+∠FBC=24°+24°=48°，根据三角形的内角和得出 ∠ACF的度数。