题目内容
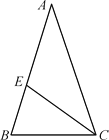
【题目】如图,△ABC中,AB=AC,∠A=36,CE平分∠ACB交AB于点E.
(1)试说明点E为线段AB的黄金分割点;
(2)若AB=4,求BC的长.
【答案】(1)证明见解析;(2)![]()
【解析】
试题(1)根据等腰三角形两底角相等求出∠ACB=72°,再根据角平分线的定义求出∠BCE=36°,从而得到∠BCE=∠A,然后判定△ABC和△CBE相似,根据相似三角形对应边成比例列出比例式整理,并根据黄金分割点的定义即可得证;
(2)根据等角对等边的性质可得AE=CE=BC,再根据黄金分割求解即可.
试题解析:(1)证明:∵AB=AC,∠A=36°,
∴∠ACB=![]() (180°-36°)=72°,
(180°-36°)=72°,
∵CE平分∠ACB,
∴∠BCE=![]() ∠ACB=
∠ACB=![]() ×72°=36°,
×72°=36°,
∴∠BCE=∠A=36°,
∴AE=BC,
又∵∠B=∠B,
∴△ABC∽△CBE,
∴![]() ,
,
∴BC2=ABBE,
即AE2=ABBE,
∴E为线段AB的黄金分割点;
(2)∵AB=AC,∠A=36°,
∴∠B=∠ACB=72°,
∴∠BEC=180°-72°-36°=72°,
∴BC=CE,
由(1)已证AE=CE,
∴AE=CE=BC,
∴BC=![]() AB=
AB=![]() ×4=2
×4=2![]() -2.
-2.

练习册系列答案
相关题目