��Ŀ����
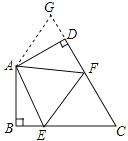
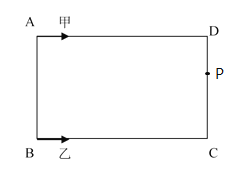
����Ŀ����ͼ���ס�����λͬѧ�ڳ����εij���ABCD�����������ܲ���������A��D��C��B��A����ѭ���ܲ���ͬʱ������B��C��D��A��B����ѭ���ܲ���AB��30�ף�BC��50�ף������ٶ�Ϊ2��/�룬���ٶ�3��/�룮
��1���辭����ʱ��Ϊt�룬���ú�t�Ĵ���ʽ��ʾ��·��Ϊ �ף�
��2�����ס������˵�һ������ʱ������������ʱ��tΪ�����룿
��3������Ϊ����A��B��C��D��A�ķ���ѭ���ܲ���������ԭ���ķ����ܲ������˵��ٶȲ��䣬�������룬���ϼף�
��4���ڣ�3���������£����ҵ�һ���ϼ�����ܲ����������پ���![]() �������ϼף���ʱ����������λ���ڵ�P��ֱ��д��
�������ϼף���ʱ����������λ���ڵ�P��ֱ��д��![]() ��ֵ����ͼ�б����P����Ҫ����д���̣�
��ֵ����ͼ�б����P����Ҫ����д���̣�

���𰸡���1��2t�ף���2��26�룻��3��130�룻��4��160��P���������.
��������
��1��ֱ�Ӹ���·��=�ٶ���ʱ��ɵã�
��2��ʱ��=·�����ٶȺͣ�![]() �룻
�룻
��3����ʱ��Ϊt�룬��3t-2t=130��
��4�����Ƴ���3�����ϵص㣬�ٸ���·�̹�ϵ�г�3a-2a=160�������ʱ�䣬���Ƴ�����ص�P.
�⣺��1����ʾ��·��Ϊ2t�ף�
��2��![]() ���룩��
���룩��
�𣺵��ס������˵�һ������ʱ������������ʱ��tΪ26��.
��3����ʱ��Ϊt�룬��
3t-2t=130
���t=130
�𣺾���130�룬���ϼ�.
��4��130��2=260���ף�
260-��50+30����2=100���ף�
100-80=20���ף�
���ԣ�3�������ϼĵص���CD�ϣ���C��20�ĵط���
�����ٴ��ϼ�ʱ��Ϊa��,��
3a-2a=160
���a=160
160��2=320���ף�
320��160=2��Ȧ��
���Եڶ������ϼĵط�����3��һ������CD�ϣ���C��20�ĵط���
P����ͼ

 �п������п��Ծ����ϵ�д�
�п������п��Ծ����ϵ�д� ��������״Ԫ��ϵ�д�
��������״Ԫ��ϵ�д� �ƸԿ�����ҵ��ϵ�д�
�ƸԿ�����ҵ��ϵ�д�