题目内容
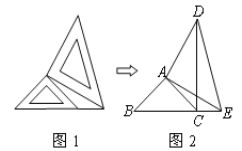
【题目】已知点D,E,F分别是△ABC的边AB,AC,BC上的点,DE∥BC,DF∥AC.
(1)如图1,点G是线段FD延长线上一点,连接EG,∠CEG的平分线EM交AB于点M,交FD于点N.则∠A,∠AME,∠CEG之间存在怎样的数量关系?请写出证明过程;
(2)如图2,在(1)的条件下,若EG平分∠AED,∠AME=35°,且∠EDF﹣∠A=30°,求∠C的度数.

【答案】(1)∠CEG=2∠A+2∠AME,证明详见解析;(2)68°.
【解析】
(1)利用外角定理即可求解;
(2)由平角AEC得:∠CEM+∠MED+∠DEA=180°,即:2α+γ+α+γ=180°;利用∠EDF﹣∠A=30°,得:2α﹣∠A=30°;利用∠CEM=∠AME=∠A,即可求解.
解:(1)∠CEM=∠A+∠AME,
而∠CEG=2∠CEM=2∠A+2∠AME;
(2)EG平分∠AED,设:∠GEA=∠GED=α,
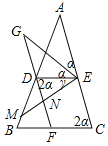
DF∥AC,则∠EDF=2α,
由平角AEC得:∠CEM+∠MED+∠DEA=180°,
即:2α+γ+α+γ=180°…①,
∠EDF﹣∠A=30°,则2α﹣∠A=30°…②,
∠CEM=∠AME=∠A,
即:35°+∠A=α+γ…③,
联立①②③并解得:α=34°,
∠C=2α=68°.

练习册系列答案
相关题目