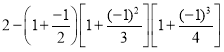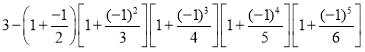题目内容
【题目】边长为2的正方形ABCD中E是AB的中点,P在射线DC上从D出发以每秒1个单位长度的速度运动,过P做PF⊥DE,当运动时间为__________秒时,以点P、F、E为顶点的三角形与△AED相似

【答案】1或![]()
【解析】∵四边形ABCD是正方形,PF⊥DE,
∴∠A=∠DFP=∠ADC=90°,
∴∠ADE+∠EDP=∠EDP+∠DPF=90°,
∴∠ADE=∠FPD,
∴△ADE∽△FPD.
(1)如图1,当∠DPE=90°时,易得△FPD∽△FEP,则△ADE∽△FEP,
此时四边形AEPD是矩形,
∴DP=AE=1,
∴t=1,即当t=1时,△ADE∽△FEP;
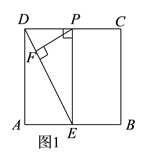
(2)如图2,当DP=EP时,易得△FPE≌△FPD,则△FEP∽△ADE,
此时四边形AEHD是矩形,
∴DH=AE=1,HP=x-1,HE=AD=2,
∴PE2=HE2+HP2=PD2,
∴![]() ,解得:
,解得: ![]() ;
;

综上所述,当![]() 或
或![]() 时,以点P、F、E为顶点的三角形与△AED相似.
时,以点P、F、E为顶点的三角形与△AED相似.
故答案为:1或![]() .
.

练习册系列答案
相关题目