题目内容
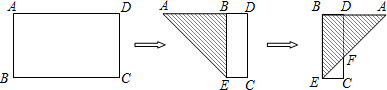
如图，有一张矩形纸片ABCD，AB=2.5，AD=1.5，将纸片折叠，使AD边落在AB边上，折痕为AE，再将△AED以DE为折痕向右折叠，AE与BC交于点F，则CF的长为
分析：利用折叠的性质，即可求得BD的长与图3中AB的长，又由相似三角形的对应边成比例，即可求得BF的长，则由CF=BC-BF即可求得答案．
解答：解：如图2，根据题意得：BD=AB-AD=2.5-1.5=1，
如图3，AB=AD-BD=1.5-1=0.5，
∵BC∥DE，
∴△ABF∽△ADE，
∴
=
，
即
=
，
∴BF=0.5，
∴CF=BC-BF=1.5-0.5=1．
故答案为：1．
如图3，AB=AD-BD=1.5-1=0.5，
∵BC∥DE，
∴△ABF∽△ADE，
∴
| AB |
| AD |
| BF |
| DE |
即
| 0.5 |
| 1.5 |
| BF |
| 1.5 |
∴BF=0.5，
∴CF=BC-BF=1.5-0.5=1．
故答案为：1．
点评：本题考查了翻折变换及正方形的性质，利用了折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等及正方形的性质，平行线的性质，有一定的难度．
练习册系列答案
相关题目
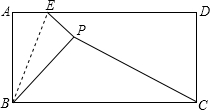（2013•吉安模拟）如图，有一张矩形纸片ABCD，已知AB=2，BC=4，若点E是AD上的一个动点（与点A不重合），且0＜AE≤2，沿BE将△ABE对折后，点A落到点P处，连接PC．
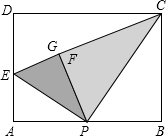如图，有一张矩形纸片ABCD，AB=4，AD=3，P为AB中点，点E在AD上，将△PBC，△PAE翻折分别得到△PCF和△PEG，折痕分别为PC、PE，且点F在PG上，则AE长为