题目内容
 (2013•吉安模拟)如图,有一张矩形纸片ABCD,已知AB=2,BC=4,若点E是AD上的一个动点(与点A不重合),且0<AE≤2,沿BE将△ABE对折后,点A落到点P处,连接PC.
(2013•吉安模拟)如图,有一张矩形纸片ABCD,已知AB=2,BC=4,若点E是AD上的一个动点(与点A不重合),且0<AE≤2,沿BE将△ABE对折后,点A落到点P处,连接PC.(1)下列说法正确的序号是
①②④
①②④
①.△ABE与△PBE关于直线BE对称
②.以B为圆心、BA的长为半径画弧交BC于H,则点P在AH上(点A除外)
③.线段PC的长有可能小于2.
④.四边形ABPE有可能为正方形
(2)试求下列情况下的线段PC的长(可用计算器,精确到0.1).
①以P、C、D为顶点的三角形是等腰三角形;
②直线CP与BE垂直.
分析:(1)根据折叠的性质,以及圆的定义即可作出判断;
(2)①以P、C、D为顶点的等腰三角形有两种情况,点P与BC的中点H重合时和点P在CD的中垂线上两种情况进行讨论,设DC的中点为K,过P作PF⊥BC于F,利用勾股定理即可求得PC的长;
②设CP⊥BE于G,则△PGB∽△BPE,△EAB∽△BGC,根据三角形的对应边的比相等即可求解.
(2)①以P、C、D为顶点的等腰三角形有两种情况,点P与BC的中点H重合时和点P在CD的中垂线上两种情况进行讨论,设DC的中点为K,过P作PF⊥BC于F,利用勾股定理即可求得PC的长;
②设CP⊥BE于G,则△PGB∽△BPE,△EAB∽△BGC,根据三角形的对应边的比相等即可求解.
解答: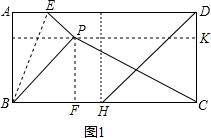 解:(1)①根据折叠的性质可得△ABE与△PBE关于直线BE对称,则正确;
解:(1)①根据折叠的性质可得△ABE与△PBE关于直线BE对称,则正确;
②根据BA=BP=BH可得:点P在弧AH上;
③当AE=AB=2时,PC的长度最小,此时P在BC上,则PC=2,四边形ABPE是正方形,故③错误,④正确.
(2)①以P、C、D为顶点的等腰三角形有两种情况.
第1种情况:如答图1,点P与BC的中点H重合时:CH=CD.
即PC=CH=2;
第2种情况:点P在CD的中垂线上时,PD=PC,设DC的中点为K,过P作PF⊥BC于F,
则四边形PFCK是矩形,PF=CK=1,PB=2.
∴BF=
,
∴FC=4-
,
PC2=(4-
)2+12,
∴PC≈2.5.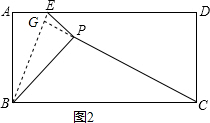
②如答图2,设CP⊥BE于G,
∵BP⊥EP.
∴△PGB∽△BPE.
=
∴BG•BE=4…①
又∵∠AEB=∠EBC,∠EAB=∠BGC=90°,△EAB∽△BGC
∴
=
,
BE•BG=4•AE…②
由①、②得AE=1
∴PE=AE=1,
∴BE=
,BG=
=
,
又∵PG×BE×
=PE•PB×
∴PG=
,CG2=42-(
)2
∴CG=
∴PC=CG-PG=
-
=
≈2.7.
故答案是:①②④.
 解:(1)①根据折叠的性质可得△ABE与△PBE关于直线BE对称,则正确;
解:(1)①根据折叠的性质可得△ABE与△PBE关于直线BE对称,则正确;②根据BA=BP=BH可得:点P在弧AH上;
③当AE=AB=2时,PC的长度最小,此时P在BC上,则PC=2,四边形ABPE是正方形,故③错误,④正确.
(2)①以P、C、D为顶点的等腰三角形有两种情况.
第1种情况:如答图1,点P与BC的中点H重合时:CH=CD.
即PC=CH=2;
第2种情况:点P在CD的中垂线上时,PD=PC,设DC的中点为K,过P作PF⊥BC于F,
则四边形PFCK是矩形,PF=CK=1,PB=2.
∴BF=
| 3 |
∴FC=4-
| 3 |
PC2=(4-
| 3 |
∴PC≈2.5.

②如答图2,设CP⊥BE于G,
∵BP⊥EP.
∴△PGB∽△BPE.
| PG |
| BP |
| BP |
| BE |
∴BG•BE=4…①
又∵∠AEB=∠EBC,∠EAB=∠BGC=90°,△EAB∽△BGC
∴
| BE |
| BC |
| AE |
| BG |
BE•BG=4•AE…②
由①、②得AE=1
∴PE=AE=1,
∴BE=
| 5 |
| 4 |
| BE |
| 4 | ||
|
又∵PG×BE×
| 1 |
| 2 |
| 1 |
| 2 |
∴PG=
| 2 | ||
|
| 4 | ||
|
∴CG=
| 8 | ||
|
∴PC=CG-PG=
| 8 | ||
|
| 2 | ||
|
6
| ||
| 5 |
故答案是:①②④.
点评:本题考查了相似三角形的判定与性质,以及折叠的性质,以及三角形的面积的计算,根据三角形的面积求得CG是关键.

练习册系列答案
相关题目
 (2013•吉安模拟)已知圆锥如图所示放置,其主视图面积为12,俯视图的周长为6n,则该圆锥的侧面积为
(2013•吉安模拟)已知圆锥如图所示放置,其主视图面积为12,俯视图的周长为6n,则该圆锥的侧面积为