题目内容
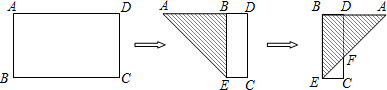
（2012•保定二模）如图，有一张矩形纸片ABCD，AD=5cm，AB=3cm，折叠使AB与AD重合，折痕AE；再将△AEB沿BE向右对折，使AE与CD相交于F，则S△CEF=
2cm2
2cm2
．分析：如第三个图，由题意易得四边形BDCE是矩形，BD=EC=2cm，AD=1cm，又由BE∥CD，根据平行线分线段成比例定理，可求得DF的长，则可求得△CEF的面积．
解答：解：∵四边形ABCD是矩形，
∴CD=AB=3cm，∠D=∠C=∠ABC=90°，
如第二个图：由折叠的性质可得：∠ABE=90°，BD=AD-AB=5-3=2（cm），
∴四边形BDCE是矩形，
∴BE=CD=3cm，BE∥CD，EC=BD=2cm，
如第三个图，AD=AB-BD=3-2=1（cm），
∵BE∥CD，
∴
=
，
即
=
，
∴DF=1cm，
∴CF=CD-DF=2（cm），
∴S△CEF=
EC•CF=
×2×2=2（cm2）．
故答案为：2cm2．
∴CD=AB=3cm，∠D=∠C=∠ABC=90°，
如第二个图：由折叠的性质可得：∠ABE=90°，BD=AD-AB=5-3=2（cm），
∴四边形BDCE是矩形，
∴BE=CD=3cm，BE∥CD，EC=BD=2cm，
如第三个图，AD=AB-BD=3-2=1（cm），
∵BE∥CD，
∴
| DF |
| BE |
| AD |
| AB |
即
| DF |
| 3 |
| 1 |
| 3 |
∴DF=1cm，
∴CF=CD-DF=2（cm），
∴S△CEF=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为：2cm2．
点评：此题考查了矩形的判定与性质、折叠的性质以及平行线分线段成比例定理．此题难度适中，注意掌握折叠前后图形的对应关系，注意数形结合思想的应用．
练习册系列答案
相关题目
（2012•保定二模）有四张不透明的卡片（如图），除正面的数字不同外，其余都相同，现将它们背面向上洗匀，从中任意抽取两张，上面的数字之和恰好为零的概率为（ ）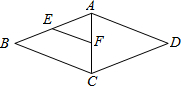
（2012•保定二模）如图所示，在菱形ABCD中，点E，F分别为AB，AC的中点，菱形ABCD的周长为32，则EF的长等于（ ）
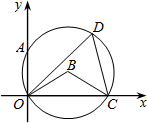（2012•保定二模）如图，⊙B过平面直角系的原点O，交y轴于点A，交x轴于点C，∠ODC=60°，A（0，2），则弦OC的长为（ ）