题目内容
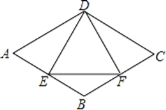
【题目】在△ABC中,∠B=60°,D、E分别为AB、BC上的点,且AE、CD交于点F.
(1)如图1,若AE、CD为△ABC的角平分线:
①求∠AFD的度数;
②若AD=3,CE=2,求AC的长;
(2)如图2,若∠EAC=∠DCA=30°,求证:AD=CE.

【答案】(1)①60°;②5;(2)详见解析.
【解析】
(1)①根据角平分线的定义、三角形内角和定理计算;
②在AC上截取AG=AD=3,连接FG,证明△ADF≌△AGF、△CGF≌△CEF,根据全等三角形的性质解答;
(2)在AE上截取FH=FD,连接CH,证明△ADF≌△CHF,根据全等三角形的性质、三角形的外角的性质解答.
解:(1)①∵AE、CD分别为△ABC的角平分线,
∴∠FAC=![]() ∠BAC,∠FCA=
∠BAC,∠FCA=![]() ∠BCA,
∠BCA,
∵∠B=60°
∴∠BAC+∠BCA=120°,
∴∠AFC=180﹣∠FAC﹣∠FCA=180﹣![]() (∠BAC+∠BCA)=120°
(∠BAC+∠BCA)=120°
∴∠AFD=180°-∠AFC=60°;
②在AC上截取AG=AD=3,连接FG,
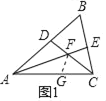
∵AE、CD分别为△ABC的角平分线,
∴∠FAC=∠FAD,∠FCA=∠FCE,
∵∠AFC=120°,
∴∠AFD=∠CFE=60°,
在△ADF和△AGF中,
∵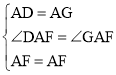 ,
,
∴△ADF≌△AGF(SAS),
∴∠AFD=∠AFG=60°,
∴∠GFC=∠CFE=60°,
在△CGF和△CEF中,
∵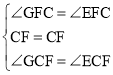 ,
,
∴△CGF≌△CEF(ASA),
∴CG=CE=2,
∴AC=5;
(2)在AE上截取FH=FD,连接CH,
∵∠FAC=∠FCA=30°,
∴FA=FC,
在△ADF和△CHF中,
∵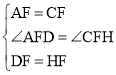 ,
,
∴△ADF≌△CHF(SAS),
∴AD=CH,∠DAF=∠HCF,
∵∠CEH=∠B+∠DAF=60°+∠DAF,
∠CHE=∠HAC+∠HCA=60°+∠HCF,
∴∠CEH=∠CHE,
∴CH=CE,
∴AD=CE.

【题目】假如你的母亲开了一家服装店,专门卖羽绒服,下面是去年一年各月销售情况表:
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
销量(件) | 100 | 90 | 50 | 11 | 8 | 6 | 4 | 6 | 5 | 30 | 80 | 110 |
根据上表,回答下列问题:
(1)计算去年各季度的销售情况,并用一幅适当的统计图表示;
(2)计算去年各季度销售量在全年销售总量中所占的百分比,并用适当的统计图表示;
(3)从这些统计图表中,你能得出什么结论?为你母亲今后的决策能提供什么有用的帮助?