题目内容
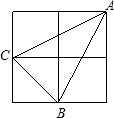如图，小正方形的边长为2，连接小正方形的三个顶点，可得到△ABC，则AC边上的高是
- A.
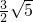
- B.
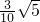
- C.
- D.
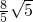
C
分析：根据勾股定理求出AC的长，再利用三角形的面积求出三角形的高即可．
解答：
解：∵小正方形的边长为2，
∴AC=
=2
，
∴S△ABC=4×4-
×2×2-×2×4-×2×4=6，
S△ABC=×AC×BD，
=×2BD=6，
解得：BD=
．
故选C．
点评：此题主要考查了勾股定理以及三角形的面积，根据题意得出△ABC的面积等于正方形面积减去其他3个三角形的面积是解决问题的关键．
分析：根据勾股定理求出AC的长，再利用三角形的面积求出三角形的高即可．
解答：
解：∵小正方形的边长为2，∴AC=
=2，∴S△ABC=4×4-
×2×2-×2×4-×2×4=6，S△ABC=
×AC×BD，=
×2BD=6，解得：BD=
．故选C．
点评：此题主要考查了勾股定理以及三角形的面积，根据题意得出△ABC的面积等于正方形面积减去其他3个三角形的面积是解决问题的关键．
练习册系列答案
相关题目
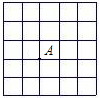如图，小正方形的边长为1，若以A为顶点的等腰直角三角形的面积为| 5 |
| 2 |
| A、4个 | B、8个 |
| C、12个 | D、16个 |
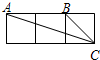如图，小正方形的边长均为1，则下面图中的三角形（阴影部分）与△ABC相似的是（ ）
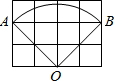（2012•北塘区二模）如图，小正方形的边长均为1，扇形OAB是某圆锥的侧面展开图，则这个圆锥的底面周长为（ ）
如图，小正方形的边长为1，试在图中作出2条长度不是有理数的线段和两条长度是有理数的线段．