题目内容
如图,抛物线y=x2-2x+c的顶点A在直线l:y=x-5上.
(1)求抛物线顶点A的坐标;
(2)设抛物线与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),试判断△ABD的形状.
(1)A(1,-4) (2)△ABD是直角三角形
解析解:(1)∵顶点 A的横坐标为x=-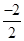 =1,
=1,
且顶点A在y=x-5上,
∴当x=1时,y=1-5=-4,∴A(1,-4).
(2)△ABD是直角三角形.
将A(1,-4)代入y=x2-2x+c,
可得1-2+c=-4,
∴c=-3,∴y=x2-2x-3,∴B(0,-3).
当y=0时,x2-2x-3=0,得x1=-1,x2=3,
∴C(-1,0),D(3,0).
∵BD2=OB2+OD2=18,
AB2=(4-3)2+12=2,AD2=(3-1)2+42=20,
∴BD2+AB2=AD2,∴∠ABD=90°,
即△ABD是直角三角形.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1)。
与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1)。



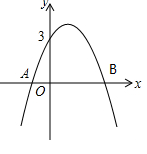
 ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).