题目内容
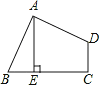
【题目】如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC于E,若线段AE=5,则S四边形ABCD=
【答案】25.
【解析】
试题分析:过A点作AF⊥CD交CD的延长线于F点,由AE⊥BC,AF⊥CF,∠C=90°可得四边形AECF为矩形,则∠2+∠3=90°,而∠BAD=90°,根据等角的余角相等得∠1=∠2,加上∠AEB=∠AFD=90°和AB=AD,根据全等三角形的判定可得△ABE≌△ADF,由全等三角形的性质有AE=AF=5,S△ABE=S△ADF,则S四边形ABCD=S正方形AECF,然后根据正方形的面积公式计算即可.
试题解析:过A点作AF⊥CD交CD的延长线于F点,如图,

∵AE⊥BC,AF⊥CF,
∴∠AEC=∠CFA=90°,
而∠C=90°,
∴四边形AECF为矩形,
∴∠2+∠3=90°,
又∵∠BAD=90°,
∴∠1=∠2,
在△ABE和△ADF中

∴△ABE≌△ADF,
∴AE=AF=5,S△ABE=S△ADF,
∴四边形AECF是边长为5的正方形,
∴S四边形ABCD=S正方形AECF=52=25.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目