题目内容
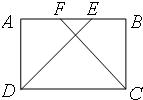24、已知：如图所示，在矩形ABCD中，AF=BE．求证：DE=CF．
分析：要证明DE=CF，只要证明△ADE≌△BCF即可．根据全等三角形的判定定理，可以得出结论．
解答：证明：∵矩形ABCD，
∴∠A=∠B、AD=BC，
∵AF=BE，
∴AE=BF，
∴△ADE≌△BCF（SAS）．
∴DE=CF．
∴∠A=∠B、AD=BC，
∵AF=BE，
∴AE=BF，
∴△ADE≌△BCF（SAS）．
∴DE=CF．
点评：本题考查了矩形的性质，各内角为90°，对边相等．根据三角形全等的判定定理求出全等三角形，是证明线段相等的常用方法．
练习册系列答案
一线名师权威作业本系列答案
相关题目
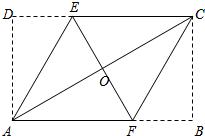21、已知：如图所示，在矩形ABCD中，分别沿AE、CF折叠△ADE、△CBF，使得点D、点B都重合于点O，且E、O、F三点共线，A、O、C三点共线．
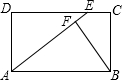已知：如图所示，在矩形ABCD中，E为DC上的一点，BF⊥AE于点F，且BF=BC，求证：AE=AB．
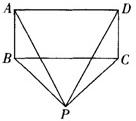34、根据要求拟编一道新题．
已知：如图所示，在矩形ABCD中，EF⊥AC分别交DC、AB于点E、F，CF∥AE，CF平分∠ACB．