题目内容
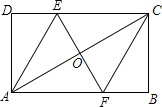 已知:如图所示,在矩形ABCD中,EF⊥AC分别交DC、AB于点E、F,CF∥AE,CF平分∠ACB.
已知:如图所示,在矩形ABCD中,EF⊥AC分别交DC、AB于点E、F,CF∥AE,CF平分∠ACB.(1)求证:△AOE≌△CBF;
(2)试说明:如何把△AOE进行合适的变换得到△CBF?
分析:(1)根据已知求出∠EAC=∠BCF,根据矩形的性质推出AE=CF,根据AAS即可推出答案;
(2)根据中心对称的性质作△AOE关于O的对称图形,再延CF翻折即可.
(2)根据中心对称的性质作△AOE关于O的对称图形,再延CF翻折即可.
解答:(1)证明:∵CF∥AE,
∴∠EAC=∠ACF,
∵CF平分∠ACB,
∴∠BCF=∠ACF,
∴∠EAC=∠BCF,
∵矩形ABCD,
∴CD∥AB,∠B=90°,
∵AE∥CF,
∴四边形AECF是平行四边形,
∴AE=CF,
∵EF⊥AC,
∴∠EOA=90°=∠B,
在△AOE和△CBF中
,
∴△AOE≌△CBF.
(2)先把△AOE绕着点O旋转180°后得到△COF,再把△COF沿直线CF翻折,即可得到△CBF.
∴∠EAC=∠ACF,
∵CF平分∠ACB,
∴∠BCF=∠ACF,
∴∠EAC=∠BCF,
∵矩形ABCD,
∴CD∥AB,∠B=90°,
∵AE∥CF,
∴四边形AECF是平行四边形,
∴AE=CF,
∵EF⊥AC,
∴∠EOA=90°=∠B,
在△AOE和△CBF中
|
∴△AOE≌△CBF.
(2)先把△AOE绕着点O旋转180°后得到△COF,再把△COF沿直线CF翻折,即可得到△CBF.
点评:本题主要考查对矩形的性质,平行四边形的性质和判定,全等三角形的判定,翻折变换,旋转性质等知识点的理解和掌握,能综合运用这些性质进行推理是解此题的关键.

练习册系列答案
相关题目
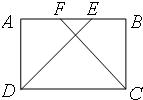 24、已知:如图所示,在矩形ABCD中,AF=BE.
24、已知:如图所示,在矩形ABCD中,AF=BE.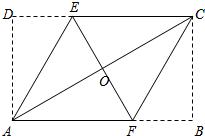 21、已知:如图所示,在矩形ABCD中,分别沿AE、CF折叠△ADE、△CBF,使得点D、点B都重合于点O,且E、O、F三点共线,A、O、C三点共线.
21、已知:如图所示,在矩形ABCD中,分别沿AE、CF折叠△ADE、△CBF,使得点D、点B都重合于点O,且E、O、F三点共线,A、O、C三点共线.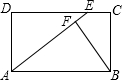 已知:如图所示,在矩形ABCD中,E为DC上的一点,BF⊥AE于点F,且BF=BC,求证:AE=AB.
已知:如图所示,在矩形ABCD中,E为DC上的一点,BF⊥AE于点F,且BF=BC,求证:AE=AB.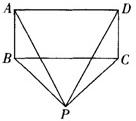 34、根据要求拟编一道新题.
34、根据要求拟编一道新题.