题目内容
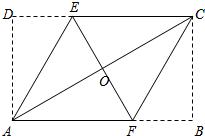21、已知：如图所示，在矩形ABCD中，分别沿AE、CF折叠△ADE、△CBF，使得点D、点B都重合于点O，且E、O、F三点共线，A、O、C三点共线．求证：四边形AFCE是菱形．
分析：根据菱形的性质，先证明四边形AFCE是平行四边形，然后根据菱形的对角线平分且相互垂直证明是菱形．
解答：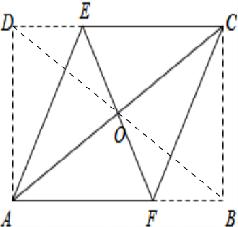
证明：如图所示：
矩形ABCD中BD于AC互相平分，所以OD=OB，
又因为DE∥BF，∠DEO=∠BFO，而且∠EOD=∠FOB，
所以△OED≌△OFB，
所以DE=PF，
又因为CD=AB，所以CF=AF，所以四边形AFCE是平行四边形；
又因为AD=AO=CO=CB，EO=FO，且∠EOA=∠ADE=90°即EF⊥AC．
所以四边形AECF是菱形．
证明：如图所示：矩形ABCD中BD于AC互相平分，所以OD=OB，
又因为DE∥BF，∠DEO=∠BFO，而且∠EOD=∠FOB，
所以△OED≌△OFB，
所以DE=PF，
又因为CD=AB，所以CF=AF，所以四边形AFCE是平行四边形；
又因为AD=AO=CO=CB，EO=FO，且∠EOA=∠ADE=90°即EF⊥AC．
所以四边形AECF是菱形．
点评：本题考查相似三角形的应用以及菱形性质的考查．
练习册系列答案
阅读快车系列答案
相关题目
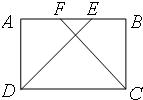24、已知：如图所示，在矩形ABCD中，AF=BE．
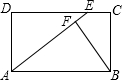已知：如图所示，在矩形ABCD中，E为DC上的一点，BF⊥AE于点F，且BF=BC，求证：AE=AB．
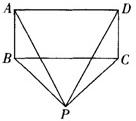34、根据要求拟编一道新题．
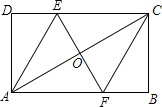已知：如图所示，在矩形ABCD中，EF⊥AC分别交DC、AB于点E、F，CF∥AE，CF平分∠ACB．