题目内容
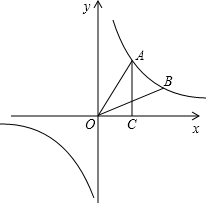 如图,点A、B在反比例函数y=
如图,点A、B在反比例函数y=| k | x |
(1)求该反比例函数的解析式;
(2)若点(-a,y1),(-2a,y2)在该反比例函数的图象上,试比较y1与y2的大小;
(3)求△AOB的面积.
分析:(1)由S△AOC=
xy=2,设反比例函数的解析式y=
,则k=xy=4;
(2)由于反比例函数的性质是:在x<0时,y随x的增大而减小,-a>-2a,则y1<y2;
(3)连接AB,过点B作BE⊥x轴,交x轴于E点,通过分割面积法S△AOB=S△AOC+S梯形ACEB-S△BOE求得.
| 1 |
| 2 |
| k |
| x |
(2)由于反比例函数的性质是:在x<0时,y随x的增大而减小,-a>-2a,则y1<y2;
(3)连接AB,过点B作BE⊥x轴,交x轴于E点,通过分割面积法S△AOB=S△AOC+S梯形ACEB-S△BOE求得.
解答:解:(1)∵S△AOC=2,
∴k=2S△AOC=4;
∴y=
;
(2)∵k>0,
∴函数y在各自象限内随x的增大而减小;
∵a>0,
∴-2a<-a;
∴y1<y2;
(3)连接AB,过点B作BE⊥x轴,
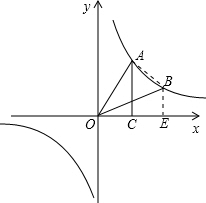
S△AOC=S△BOE=2,
∴A(a,
),B(2a,
);
S梯形=
(
+
)×(2a-a)=3,
∴S△AOB=S△AOC+S梯形ACEB-S△BOE=3.
∴k=2S△AOC=4;
∴y=
| 4 |
| x |
(2)∵k>0,
∴函数y在各自象限内随x的增大而减小;
∵a>0,
∴-2a<-a;
∴y1<y2;
(3)连接AB,过点B作BE⊥x轴,

S△AOC=S△BOE=2,
∴A(a,
| 4 |
| a |
| 2 |
| a |
S梯形=
| 1 |
| 2 |
| 2 |
| a |
| 4 |
| a |
∴S△AOB=S△AOC+S梯形ACEB-S△BOE=3.
点评:此题重点检查函数性质的应用和图形的分割转化思想.同学们要熟练掌握这类题型.

练习册系列答案
相关题目
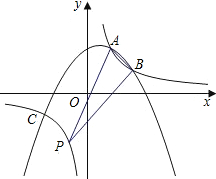 如图,抛物线y=ax2+bx+c经过点A(1,2)、B(2,1)和C(-2,-1)三点.
如图,抛物线y=ax2+bx+c经过点A(1,2)、B(2,1)和C(-2,-1)三点. 如图,△P1OA1,△P2A1A2,△P3A2A3,…,是等腰直角三角形,点P1,P2,P3,…,在反比列函数y=
如图,△P1OA1,△P2A1A2,△P3A2A3,…,是等腰直角三角形,点P1,P2,P3,…,在反比列函数y=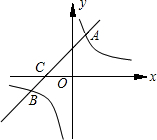 次函数y=mx+b的图象与x轴交于点C.
次函数y=mx+b的图象与x轴交于点C. 如图,△P1OA1、△P2A1A2、△P3A2A3、…、△P100A99A100是等腰直角三角形,点P1、P2、P3、…、P100在反比列函数
如图,△P1OA1、△P2A1A2、△P3A2A3、…、△P100A99A100是等腰直角三角形,点P1、P2、P3、…、P100在反比列函数