题目内容
 如图,△P1OA1,△P2A1A2,△P3A2A3,…,是等腰直角三角形,点P1,P2,P3,…,在反比列函数y=
如图,△P1OA1,△P2A1A2,△P3A2A3,…,是等腰直角三角形,点P1,P2,P3,…,在反比列函数y=| 4 | x |
分析:过点P1作P1M⊥x轴,由于△OAP1是等腰直角三角形,因而PA=OA,因而可以设P1点的坐标是(a,a),把(a,a)代入解析式即可求出a=2,因而求出P的坐标是(2,2),进一步得到OA1=4,再根据△P2A1A2是等腰直角三角形,设P2的纵坐标是b,因而横坐标是b+4,把P2的坐标代入解析式y=
,即可求出b,然后即可求出点B的坐标.
| 4 |
| x |
解答: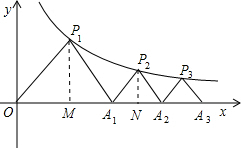 解:如图,过点P1作P1M⊥x轴于M,
解:如图,过点P1作P1M⊥x轴于M,
∵△OAP1是等腰直角三角形,
∴P1M=OM,
∴设P1点的坐标是(a,a),
把(a,a)代入解析式得到a=2,
∴P1的坐标是(2,2),
则OA1=4,
∵△P2A1A2是等腰直角三角形,过点P2作P2N⊥x轴于N,
设P2的纵坐标是b,
∴横坐标是b+4,
把P2的坐标代入解析式y=
,
∴b+4=
,
∴b=2
-2,
∴点P2的横坐标为2
+2,
∴P2点的坐标是(2
+2,2
-2),
∴点A2的坐标是(4
,0).
故答案为:(4
,0).
 解:如图,过点P1作P1M⊥x轴于M,
解:如图,过点P1作P1M⊥x轴于M,∵△OAP1是等腰直角三角形,
∴P1M=OM,
∴设P1点的坐标是(a,a),
把(a,a)代入解析式得到a=2,
∴P1的坐标是(2,2),
则OA1=4,
∵△P2A1A2是等腰直角三角形,过点P2作P2N⊥x轴于N,
设P2的纵坐标是b,
∴横坐标是b+4,
把P2的坐标代入解析式y=
| 4 |
| x |
∴b+4=
| 4 |
| b |
∴b=2
| 2 |
∴点P2的横坐标为2
| 2 |
∴P2点的坐标是(2
| 2 |
| 2 |
∴点A2的坐标是(4
| 2 |
故答案为:(4
| 2 |
点评:本题考查了反比例函数的图象画法和它的性质,利用形数结合解决此类问题,是非常有效的方法.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
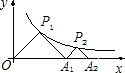 如图,△P1OA1、△P2A1A2是等腰直角三角形,点P1、P2在函数y=
如图,△P1OA1、△P2A1A2是等腰直角三角形,点P1、P2在函数y=| 4 |
| x |
A、(2
| ||
B、(2
| ||
C、(4
| ||
D、(2
|
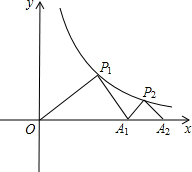 如图,△P1OA1,△P2A1A2是等腰直角三角形,点P1,P2在函数y=
如图,△P1OA1,△P2A1A2是等腰直角三角形,点P1,P2在函数y= 如图,△P1OA1、△P2A1A2、△P3A2A3、…、△P100A99A100是等腰直角三角形,点P1、P2、P3、…、P100在反比列函数
如图,△P1OA1、△P2A1A2、△P3A2A3、…、△P100A99A100是等腰直角三角形,点P1、P2、P3、…、P100在反比列函数