题目内容
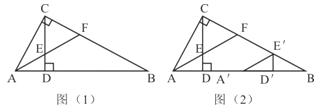
【题目】如图,△ABC是边长为4cm的等边三角形,AD为BC边上的高,点P沿BC向终点C运动,速度为1cm/s,点Q沿CA、AB向终点B运动,速度为2cm/s,若点P、Q两点同时出发,设它们的运动时间为x(s).
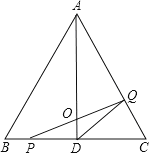
(l)求x为何值时,PQ⊥AC;x为何值时,PQ⊥AB?
(2)当O<x<2时,AD是否能平分△PQD的面积?若能,说出理由;
(3)探索以PQ为直径的圆与AC的位置关系,请写出相应位置关系的x的取值范围(不要求写出过程).
【答案】(1)当x=![]() (Q在AC上)时,PQ⊥AC;x=
(Q在AC上)时,PQ⊥AC;x=![]() 时PQ⊥AB;(2)AD平分△PQD的面积;(3)当x=
时PQ⊥AB;(2)AD平分△PQD的面积;(3)当x=![]() 或
或![]() 时,以PQ为直径的圆与AC相切,当0≤x<
时,以PQ为直径的圆与AC相切,当0≤x<![]() 或
或![]() <x<
<x<![]() 或
或![]() <x≤4时,以PQ为直径的圆与AC相交.
<x≤4时,以PQ为直径的圆与AC相交.
【解析】
试题分析:(1)若使PQ⊥AC,则根据路程=速度×时间表示出CP和CQ的长,再根据30度的直角三角形的性质列方程求解;
若使PQ⊥AB,则根据路程=速度×时间表示出BP,BQ的长,再根据30度的直角三角形的性质列方程求解;
(2)根据三角形的面积公式,要证明AD平分△PQD的面积,只需证明O是PQ的中点.根据题意可以证明BP=CN,则PD=DN,再根据平行线等分线段定理即可证明;
(3)根据(1)中求得的值即可分情况进行讨论.
试题解析:(1)当Q在AB上时,显然PQ不垂直于AC,
当Q在AC上时,由题意得,BP=x,CQ=2x,PC=4-x;
∵AB=BC=CA=4,
∴∠C=60°;
若PQ⊥AC,则有∠QPC=30°,
∴PC=2CQ,
∴4-x=2×2x,
∴x=![]() ;
;
当x=![]() (Q在AC上)时,PQ⊥AC;
(Q在AC上)时,PQ⊥AC;
如图:①
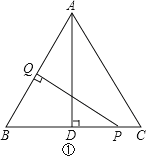
当PQ⊥AB时,BP=x,BQ=![]() x,AC+AQ=2x;
x,AC+AQ=2x;
∵AC=4,
∴AQ=2x-4,
∴2x-4+![]() x=4,
x=4,
∴x=![]() ,
,
故x=![]() 时PQ⊥AB;
时PQ⊥AB;
(2)过点QN⊥BC于点N,
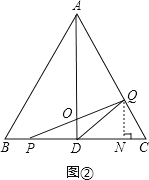
当0<x<2时,在Rt△QNC中,QC=2x,∠C=60°;
∴NC=x,
∴BP=NC,
∵BD=CD,
∴DP=DN;
∵AD⊥BC,QN⊥BC,
∴DP=DN;
∵AD⊥BC,QN⊥BC,
∴AD∥QN,
∴OP=OQ,
∴S△PDO=S△DQO,
∴AD平分△PQD的面积;
(3)显然,不存在x的值,使得以PQ为直径的圆与AC相离,
当x=![]() 或
或![]() 时,以PQ为直径的圆与AC相切,
时,以PQ为直径的圆与AC相切,
当0≤x<![]() 或
或![]() <x<
<x<![]() 或
或![]() <x≤4时,以PQ为直径的圆与AC相交.
<x≤4时,以PQ为直径的圆与AC相交.

【题目】(规律探究题)下表是按一定规律排列的一列方程,仔细观察,大胆猜想,科学推断,完成练习.
序号 | 方程 | 方程的解 |
1 | x2-2x-3=0 | x1=-1,x2=3 |
2 | x2-4x-12=0 | x1=-2,x2=6 |
3 | x2-6x-27=0 | x1=-3,x2=9 |
… | … | … |
(1)这列方程中第10个方程的两个根分别是x1=____,x2=____.
(2)这列方程中第n个方程为________.
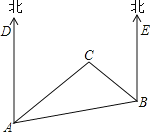
【题目】如图,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘A中放置一个重物,在右边活动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.实验数据记录如下表:
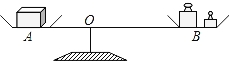
x(cm) | 10 | 15 | 20 | 25 | 30 |
y(g) | 30 | 20 | 15 | 12 | 10 |
(1)猜测y与x之间的函数关系,求出函数关系式并加以验证;
(2)当砝码的质量为24g时,活动托盘B与点O的距离是多少?
(3)将活动托盘B往左移动时,应往活动托盘B中添加还是减少砝码?