题目内容
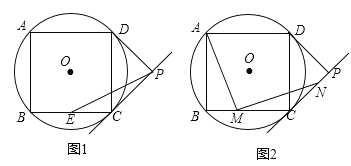
【题目】将一副直角三角板如图1,摆放在直线![]() 上(直角三角板
上(直角三角板![]() 和直角三角板
和直角三角板![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,保持三角板
,保持三角板![]() 不动,将三角板
不动,将三角板![]() 绕点
绕点![]() 以每秒5°的速度顺时针旋转,旋转时间为t秒.当
以每秒5°的速度顺时针旋转,旋转时间为t秒.当![]() 与射线
与射线![]() 意合时停止旋转.
意合时停止旋转.
(1)如图2.当![]() 为
为![]() 的角平分线时,求此时
的角平分线时,求此时![]() 的值?
的值?
(2)当![]() 旋转至
旋转至![]() 的内部时,求
的内部时,求![]() 与
与![]() 的数量关系?
的数量关系?
(3)在旋转过程中,当三角板![]() 的其中一边平行于三角板
的其中一边平行于三角板![]() 的某一边时,求此时
的某一边时,求此时![]() 等于______.(直接写出答案即可)
等于______.(直接写出答案即可)

【答案】(1)3s(2)∠ECB∠DCA=15°(3)15s或24s或27s或33s
【解析】
(1)先计算∠DCE的度数,再根据角平分线的定义和旋转的速度可得t的值;
(2)分别表示∠DCA与∠ECB的度数,相减可得数量关系;
(3)分五种情况讨论:AB分别和△DCE三边平行,还有AC∥DE,计算旋转角并根据速度列方程可得结论.
(1)如图2,∵∠EDC=90°,∠DEC=60°,
∴∠DCE=30°,
∵AC平分∠DCE,
∴∠ACE=![]() ∠DCE=15°,
∠DCE=15°,
∴t=![]() =3,
=3,
答:此时t的值是3s;
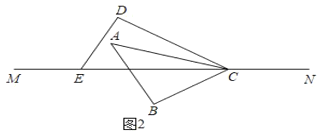
(2)当AC旋转至∠DCE的内部时,如图3,∠DCA与∠ECB的数量关系是:∠ECB∠DCA=15°;
理由是:由旋转得:∠ACE=5t,
∴∠DCA=30°5t,∠ECB=45°5t,
∴∠ECB∠DCA=(45°5t)(30°5t)=15°;
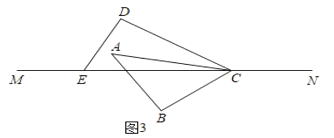
(3)分四种情况:
①当AB∥DE时,如图4,∠ACE=45°+30°=5°t,
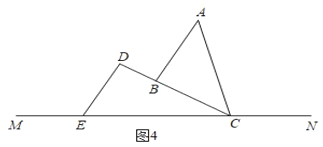
t=15;
②当AB∥CE时,如图5,则∠BCE=∠B=90°,
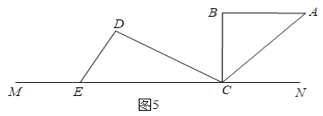
∴∠ACE=90°+45°=5°t,
t=27;
③当AB∥CD时,如图6,则∠DCB=∠B=90°,
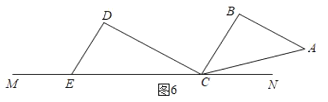
∠ACE=30°+90°+45°=5°t,
t=33;
④当AC∥DE时,如图7,
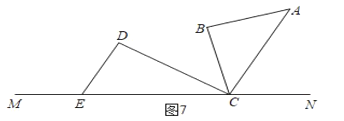
∴∠ACD=∠D=90°,
∴∠ACE=90°+30°=5°t,
t=24;
⑤当BC∥DE时,90°+30°+45°=5°t
∴t=33
综上,t的值是15s或24s或27s或33s.
故答案为:15s或24s或27s或33s.

 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案【题目】汶川地震发生后,全国人民抗震救灾,众志成城某地政府急灾民之所需,立即组织![]() 辆汽车,将
辆汽车,将![]() 三种救灾物资共
三种救灾物资共![]() 吨一次性运往灾区,假设甲、乙,丙三种车型分别运载
吨一次性运往灾区,假设甲、乙,丙三种车型分别运载![]() 三种物资,根据下表提供的信息解答下列问题:
三种物资,根据下表提供的信息解答下列问题:
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) |
|
|
|
(1)设装运![]() 品种物资的车辆数分别为
品种物资的车辆数分别为![]() 试用含
试用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)据(1)中的表达式,试求![]() 三种物资各几吨.
三种物资各几吨.