题目内容
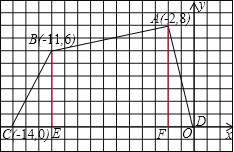
【题目】如图,四边形ABCD各顶点的坐标分别为(-2,8),(-11,6),(-14,0),(0,0).
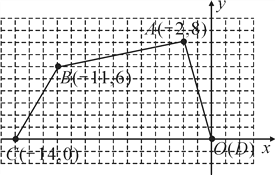
(1)确定这个四边形的面积,你是怎样做的?
(2)如果把四边形ABCD各顶点纵坐标保持不变,横坐标增加2,所得的四边形面积又是多少?
【答案】(1) 80;(2)80
解:(1) (1)S四边形ABCD=14×8-![]() ×8×2-2×3-
×8×2-2×3-![]() ×2×9-
×2×9-![]() ×3×6=112-8-6-9-9=80 (2)各顶点纵坐标保持不变,横坐标增加2,即把四边形ABCD向右平移2个单位,所以形状、大小不发生改变,面积也不变,仍是80
×3×6=112-8-6-9-9=80 (2)各顶点纵坐标保持不变,横坐标增加2,即把四边形ABCD向右平移2个单位,所以形状、大小不发生改变,面积也不变,仍是80
【解析】试题分析:(1)过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,把四边形ABCD的面积分成两个三角形的面积与梯形的面积的和,然后列式求解即可;
(2)横坐标增加2,纵坐标不变,就是把四边形ABCD向右平移2个单位,根据平移的性质,四边形的面积不变.
试题解析:(1)如图,过点A作AF⊥x轴,过点B作BE⊥x轴,
则DF=2,CE=3,AF=8,BE=6,EF=-2-(-11)=9,
四边形ABCD的面积=S△ADF+S△BCE+S梯形ABEF,
=![]() ×2×8+
×2×8+![]() ×3×6+
×3×6+![]() ×(6+8)×9,
×(6+8)×9,
=8+9+63,
=80;
(2)四边形ABCD各个顶点的纵坐标保持不变,横坐标增加4,
就是把四边形ABCD向右平移4个单位,
所以,所得的四边形的面积不变,还是80.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目