Question

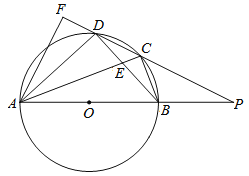
【题目】如图，四边形ABCD内接于⊙O，AB是⊙O的直径，AC和BD相交于点E，且DC2=CECA．

(1)求证：BC=CD；

(2)分别延长AB，DC交于点P，过点A作AF⊥CD交CD的延长线于点F，若PB=OB，CD=，求DF的长．

Answer 1

【答案】（1）证明见解析；

（2）DF的长为．

【解析】(1)证明：∵DC2=CECA，∴，又∠DCE=∠ACD，

∴△CDE∽△CAD，∴∠CDB=∠DAC，∴= ，∴BC=CD；

(2)解：如图，连接OC，

∵BC=CD，∴∠DAC=∠CAB，又∵AO=CO，∴∠CAB=∠ACO，

∴∠DAC=∠ACO，∴AD∥OC，∴，

∵PB=OB，CD=，∴．∴PC=4．

又∵∠P=∠P，∠PAD=∠PCB，∴△PCB∽△PAD，

∴， ∴，∴OB=4．

在Rt△ACB中，AC===2，

∵AB是直径，∴∠ADB=∠ACB=90°，

∴∠FDA+∠BDC=90°，∠CBA+∠CAB=90°，

∵∠BDC=∠CAB，∴∠FDA=∠CBA．

又∵∠AFD=∠ACB=90°，∴△AFD∽△ACB，

∴．

在Rt△AFP中，设FD=x，则AF=x，

在Rt△APF中有，，求得DF=．