题目内容
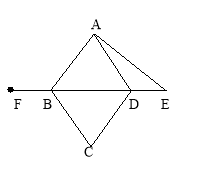
【题目】如图,在△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O逆时针方向旋转90°
得到△OA1B1 . 
(1)线段A1B1的长是 , ∠AOA1的度数是;
(2)连结AA1 , 求证:四边形OAA1B1是平行四边形;
(3)求四边形OAA1B1的面积.
【答案】
(1)6;90°
(2)解:∵A1B1=AB=6,OA1﹣OA=6,∠OA1B1=∠OAB=90°,∠AOA1=90°,
∴∠OA1B1=∠AOA1,A1B1=OA,
∴B1A1∥OA,
∴四边形OAA1B1是平行四边形
(3)解:S=OAA1O=6×6=36.
即四边形OAA1B1的面积是36
【解析】解:(1)A1B1=AB=6,∠AOA1=90°.
故答案是:6,90°;
(1)根据旋转的性质即可直接求解;(2)根据旋转的性质以及平行线的判定定理证明B1A1∥OA且A1B1=OA即可证明四边形OAA1B1是平行四边形;(3)利用平行四边形的面积公式求解.

 53随堂测系列答案
53随堂测系列答案【题目】已知抛物线y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0( ) 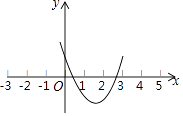
A.没有实根
B.只有一个实根
C.有两个实根,且一根为正,一根为负
D.有两个实根,且一根小于1,一根大于2
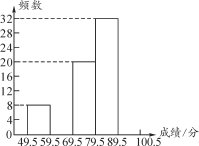
【题目】6月5日是世界环境日,为了普及环保知识,增强环保意识,某市第一中学举行了“环保知识竞赛”,参赛人数为1 000人.为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,最少为50分,得分取整数)进行统计,并绘制出不完整的频数分布表和不完整的频数分布直方图如下:
分组 | 频数 | 所占百分比 |
49.5~59.5 | 8 | 8% |
59.5~69.5 | __ __ | 12% |
69.5~79.5 | 20 | __ __ |
79.5~89.5 | 32 | __ __ |
89.5~100.5 | __ __ | 28% |
(1)补全频数分布表和频数分布直方图;
(2)若成绩在80分以上为优秀,求这次参赛的学生中成绩为优秀的约有多少人.