题目内容
【题目】已知：如图，四边形ABCD是菱形，E是BD延长线上一点，F是DB延长线上一点，且DE=BF．请你以F为一个端点，和图中已标明字母的某一点连成一条新的线段，猜想并证明它和图中已有的某一条线段相等（只须证明一组线段相等即可）．
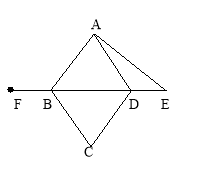
（1）连接 ；
（2）猜想： = ；
（3）证明：
【答案】（1）连结AF
（2）AF=AE
（3）证明：
∵四边形ABCD是菱形
∴AB=AD
∴∠ADB=∠ABD
∵∠ABD+∠ABF=180°
∠ADB+∠ADE=180°
∴∠ABF=∠ADE
∵BF = DE
∴△ABF≌△ADE（SAS）
∴AF=AE
【解析】
试题分析：根据观察图形，应该是连接AF或者CF
（1）连结AF（或连结CF）
（2）猜想AF=AE（连结CF的，则猜想CF=AE）
（3）证明：（以AF=AE为例，其他证法参照得分）
∵四边形ABCD是菱形
∴AB=AD
∴∠ADB=∠ABD
∵∠ABD+∠ABF=180°
∠ADB+∠ADE=180°
∴∠ABF=∠ADE
∵BF = DE
∴△ABF≌△ADE（SAS）
∴AF=AE
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
