题目内容
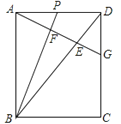
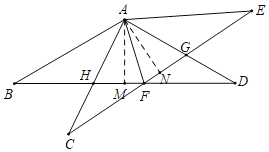
【题目】已知,如图,△ABD中,AB=AD=1,∠B=30°,△ABD绕着A点逆时针α(0°<α<120°)旋转得到△ACE.CE与AD、BD分别交于点G、F;AD、CE交于点G,设DF+GF=x,△AEG的面积为y,则y关于x的函数解析式为_____.

【答案】y=![]() (0<x<
(0<x<![]() ).
).
【解析】
设AC交BD于H,作AM⊥BD于M,AN⊥EC于N.想办法证明FG+DF=DH,求出BD,AM即可解决问题.
解:设AC交BD于H,作AM⊥BD于M,AN⊥EC于N.
∵AB=AD=1,∠B=30°,AM⊥BD,
∴AM=![]() AN=
AN=![]() ,BM=DM=
,BM=DM=![]() ,
,
∴BD=EC=![]() ,
,
∵∠BAD=∠CAE,
∴∠BAH=∠EAG,
∵AB=AE,∠B=∠E=30°,
∴△BAH≌△EAG(ASA),
∴AH=AG,BH=EG,
∵△ABD≌△ACE,
∴AM=AN,
∵∠AMH=∠ANG=90°,
∴Rt△AMH≌Rt△ANG(HL),
∴HM=GN,
∵∠AMF=∠ANF=90°,AF=AF,
∴Rt△AFM≌Rt△AFN(HL),
∴FM=FN,
∴FG=FH,
∴FG+DF=FH+DF=DH=x,
∴EG=BH=![]() ﹣x,
﹣x,
∴y=S△AEG=![]() EGAN=
EGAN=![]() ,
,
∴y=![]() (0<x<
(0<x<![]() ),
),
故答案为y=![]() (0<x<
(0<x<![]() ).
).

练习册系列答案
相关题目
【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对
他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
(计算方差的公式:s2=![]() [
[![]() ])
])