题目内容
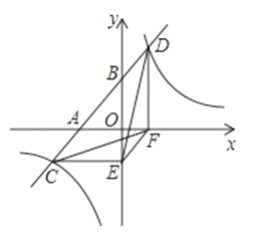
【题目】如图,一次函数y=ax+b与x轴、y轴交于A、B两点,与反比例函数y=![]() 相交于C、D两点,分别过C、D两点作y轴、x轴的垂线,垂足为E、F,连接CF、DE、EF. 有下列三个结论:①△CEF与△DEF的面积相等;②△DCE≌△CDF;③AC=BD.其中正确的结论个数是( )
相交于C、D两点,分别过C、D两点作y轴、x轴的垂线,垂足为E、F,连接CF、DE、EF. 有下列三个结论:①△CEF与△DEF的面积相等;②△DCE≌△CDF;③AC=BD.其中正确的结论个数是( )
A. 0 B. 1 C. 2 D. 3
【答案】C
【解析】
设D(x,![]() ),得出F(x,0),根据三角形的面积求出△DEF的面积,同法求出△CEF的面积,即可判断①;根据全等三角形的判定判断②即可;证出平行四边形BDFE和平行四边形ACEF,得到BD=AC即可.
),得出F(x,0),根据三角形的面积求出△DEF的面积,同法求出△CEF的面积,即可判断①;根据全等三角形的判定判断②即可;证出平行四边形BDFE和平行四边形ACEF,得到BD=AC即可.
①设D(x,![]() ),则F(x,0),由图象可知x>0,k>0,∴△DEF的面积=
),则F(x,0),由图象可知x>0,k>0,∴△DEF的面积=![]() DFOF=
DFOF=![]() k,同理可知:△CEF的面积是
k,同理可知:△CEF的面积是![]() k,∴△CEF的面积等于△DEF的面积,∴①正确;
k,∴△CEF的面积等于△DEF的面积,∴①正确;
②条件不足,无法证出两个三角形全等,∴②错误;
③∵△CEF的面积等于△DEF的面积,∴边EF上的高相等,∴CD∥EF.
∵BD∥EF,DF∥BE,∴四边形BDFE是平行四边形,∴BD=EF,同理EF=AC,∴AC=BD,∴③正确;正确的有2个.
故选C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目