Question

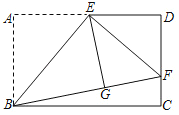
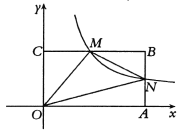
【题目】如图，在平面直角坐标系中，矩形的顶点、分别在、轴的正半轴上，顶点的坐标为．点是边上的一个动点(不与、重合)，反比例函数 的图象经过点且与边交于点，连接．

（1）当点是边的中点时，求反比例函数的表达式

（2）在点的运动过程中，试证明：是一个定值．

Answer 1

【答案】（1）y=；（2）2

【解析】

（1）根据已知条件，求出点的坐标，代入反比例函数解析式即可求出；

（2）根据待定系数法，可得反比例函数解析式，根据自变量与函数值的对应关系，可得点N的坐标，根据线段的和差可得MB、BN，再根据分式的性质可得答案．

解：（1）矩形的顶点、分别在、轴的正半轴上，顶点的坐标为．

∵点是边的中点，∴点的坐标为，

∵反比例函数 的图象经过点，

∴ ，解得：

∴反比例函数的表达式为．

（2）证明：设点M的坐标为，

∴．

∵反比例函数 的图象经过点，

∴，

∵反比例函数 的图象经过点且与边交于点，

∴点的横坐标是，

当时，，

∴点的坐标是．

∴，

∵，

∴是一个定值．