题目内容
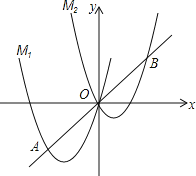
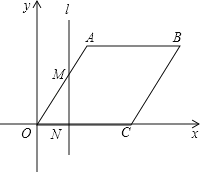
【题目】如图,在平面直角坐标系中,四边形OABC为菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线l与菱形OABC的两边分别交于点M、N(点M在点N的上方).
(1)求A、B两点的坐标;
(2)设△OMN的面积为S,直线l运动时间为t秒(0≤t≤6),试求S与t的函数表达式;
(3)在题(2)的条件下,是否存在某一时刻,使得△OMN的面积与OABC的面积之比为3:4?如果存在,请求出t的取值;如果不存在,请说明理由.
【答案】(1)A(2,2![]() ),B(6,2
),B(6,2![]() );(2)S=
);(2)S=![]() t2;S=
t2;S=![]() t;S=﹣
t;S=﹣![]() t2+3
t2+3![]() t;(3)不存在,理由见解析;不存在某一时刻,使得△OMN的面积与OABC的面积之比为3:4.
t;(3)不存在,理由见解析;不存在某一时刻,使得△OMN的面积与OABC的面积之比为3:4.
【解析】
(1)根菱形性质得出OA=AB=BC=CO=4,过A作AD⊥OC于D,求出AD、OD,即可得出答案;
(2)有三种情况:①当0≤t≤2时,直线l与OA、OC两边相交,②当2<t≤4时,直线l与AB、OC两边相交,③当4<t≤6时,直线l与AB、BC两边相交,画出图形求出即可;
(3)分为以上三种情况,求出得到的方程的解,看看是否在所对应的范围内,即可进行判断.
解:(1)∵四边形OABC为菱形,点C的坐标是(4,0),
∴OA=AB=BC=CO=4,
过A作AD⊥OC于D,
∵∠AOC=60°,
∴OD=2,AD=![]() ,
,
∴A(2,![]() ),B(6,
),B(6,![]() );
);
(2)直线l从y轴出发,沿x轴正方向运动与菱形OABC的两边相交有三种情况:①如图1,
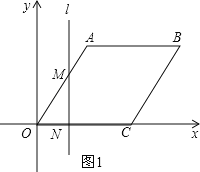
当0≤t≤2时,直线l与OA、OC两边相交,
∵MN⊥OC,
∴ON=t,
∴MN=ONtan60°=![]() t,
t,
∴S=![]() ONMN=
ONMN=![]() t2;
t2;
②当2<t≤4时,直线l与AB、OC两边相交,如图2,
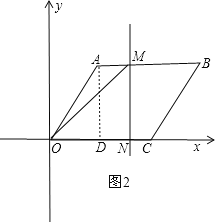
S=![]() ONMN=
ONMN=![]() ×t×
×t×![]() =
=![]() t;
t;
③当4<t≤6时,直线l与AB、BC两边相交,如图3,
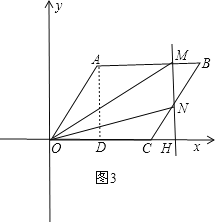
设直线l与x轴交于H,
MN=![]() ,
,
∴S=![]() MNOH=
MNOH=![]() (t
(t![]() )t=
)t=![]() ;
;
(3)答:不存在,
理由是:假设存在某一时刻,使得△OMN的面积与OABC的面积之比为3:4,
菱形AOCB的面积是4×2![]() =8
=8![]() ,
,
①![]() t2:8
t2:8![]() =3:4,
=3:4,
解得:t=±2![]() ,
,
∵0≤t≤2,
∴此时不符合题意舍去;
②![]() t:8
t:8![]() =3:4,
=3:4,
解得:t=6(舍去);
③(![]() ):8
):8![]() =3:4,
=3:4,
此方程无解.
综合上述,不存在某一时刻,使得△OMN的面积与OABC的面积之比为3:4.