题目内容
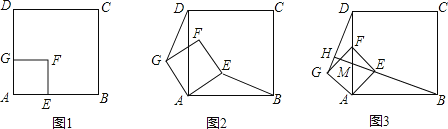
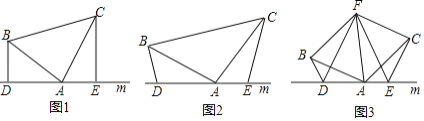
【题目】如图(1),已知:在![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,
,![]() 直线
直线![]() ,
,![]() 直线
直线![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]() .证明:
.证明:![]() .
.
(2)如图(2),将(1)中的条件改为:在![]() 中,
中,![]() ,
,![]() 、
、![]() 、
、![]() 三点都在直线
三点都在直线![]() 上,并且有
上,并且有![]() .请直接写出线段
.请直接写出线段![]() 、
、![]() 和
和![]() 之间的数量关系.
之间的数量关系.
(3)拓展与应用:如图(3),![]() 、
、![]() 是
是![]() 、
、![]() 、
、![]() 三点所在直线
三点所在直线![]() 上的两动点
上的两动点![]() 、
、![]() 、
、![]() 三点互不重合),点
三点互不重合),点![]() 为
为![]() 平分线上的一点,且
平分线上的一点,且![]() 和
和![]() 均为等边三角形,连接
均为等边三角形,连接![]() 、
、![]() ,若
,若![]() ,试证明
,试证明![]() .
.
【答案】(1)证明见解析;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)由“一线三垂直”模型,得![]() ,进而,即可得到结论;
,进而,即可得到结论;
(2)由“一线三等角”模型,得![]() ,进而,即可得到结论;
,进而,即可得到结论;
(3)由等边三角形锝性质结合条件,得![]() ,从而得
,从而得![]() ,进而得
,进而得![]() ,
,![]() ,结合条件,易证
,结合条件,易证![]() ,即可得到结论.
,即可得到结论.
(1)![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
∵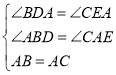 ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ;
;
(2)![]() ,理由如下:
,理由如下:
![]() ,
,
![]() ,
,
![]() .
.
在![]() 和
和![]() 中
中
∵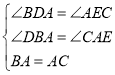 ,
,
![]() ,
,
![]() ,
,![]()
![]() ;
;
(3)![]() 和
和![]() 均为等边三角形,
均为等边三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,
∵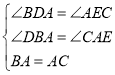 ,
,
![]() ,
,
![]() ,
,![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
在![]() 和
和![]() 中
中
∵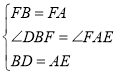 ,
,
![]() ,
,
![]() .
.

练习册系列答案
相关题目