题目内容
【题目】在探究两个三角形满足两边和其中一边的对角对应相等(“SSA”)是否能判定两个三角形全等时,我们设计不同情形进行探究:
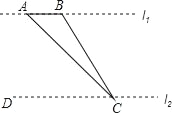
(1)例如,当∠B 是锐角时,如图 ,BC=EF,∠B=∠E,在射线 EM 上有点 D,使 DF=AC,用尺规画出符合条件的点 D,则△ABC 和△DEF 的关系是( );
A.全等 B. 不全等 C. 不一定全等

我们进一步发现如果能确定这两个三角形的形状,那么“SSA”是成立的.
(2)例如,已知:如图,在锐角△ABC 和锐角△DEF 中,AC=DF,BC=EF,∠B=∠E. 求证:△ABC≌△DEF.

【答案】(1) C(2)证明详见解析
【解析】
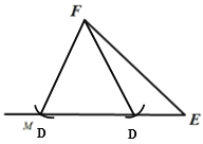
(1)以F为圆心,FD为半径画弧,则交ME两点,这两点都满足要求.其中只有形状为锐角三角形的与原三角形相似.
(2)根据(1)可知,已经确定两个三角形为锐角三角形,则可用两边和其中一边的对角对应相等的两个三角形全等.
(1)如图所示,以F为圆心,FD为半径,则这样的D点有两个.则△ABC 和△DEF 的关系是不一定全等.
(2)在△ABC与△DEF中
有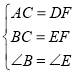
且△ABC和△DEF是锐角三角形
则△ABC≌△DEF.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目